# 一、什么是弹性力和阻尼力

弹簧力方向与位移变化量的大小成正比，方向相反

阻尼力方向与速度变化量的大小成正比，方向相反

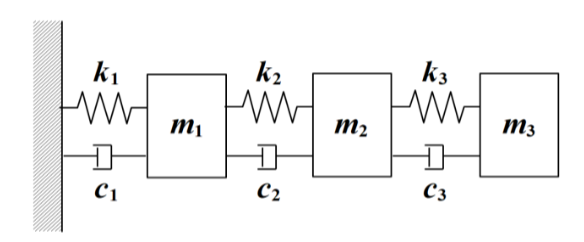
# 二、3 自由度弹簧 - 阻尼器 - 质量系统

3 自由度弹簧 - 阻尼 - 质量系统结构图如下图所示

使用数轴建模法建立的动力学方程为

$$\left\{\begin{matrix} m_{1}\ddot{x}_{1}=-k_{1}x_{1}-c_{1}\dot{x}_{1}-k_{2}\left(x_{1}-x_{2}\right)-c_{2}\left(\dot{x}_{1}-\dot{x}_{2}\right)+u_{1}\\ m_{2}\ddot{x}_{2}=k_{2}\left(x_{1}-x_{2}\right)+c_{2}\left(\dot{x}_{1}-\dot{x}_{2}\right)-k_{3}\left(x_{2}-x_{3}\right)-c_{3}\left(\dot{x}_{2}-\dot{x}_{3}\right)+u_{2}\\ m_{3}\ddot{x}_{3}=k_{3}\left(x_{2}-x_{3}\right)+c_{3}\left(\dot{x}_{2}-\dot{x}_{3}\right)+u_{3} \end{matrix}\right.$$

其中 $x_{1}\space$，$x_{2}\space$，$x_{3}\space$ 分别为各质量块相对初始位置向右的位移，$u_{1}\space$、$u_{2}\space$、$u_{3}\space$ 分别为作用在各质量块上方向向右的力，基于该动力学方程可建立系统的状态空间方程为

$$\left\{\begin{matrix} \begin{bmatrix} \dot{x}_{1} \\ \dot{x}_{2}\\ \dot{x}_{3}\\ \ddot{x}_{1}\\ \ddot{x}_{2}\\ \ddot{x}_{3} \end{bmatrix}= \begin{bmatrix} 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ -\frac{k_{1}+k_{2}}{m_{1}} & \frac{k_{2}}{m_{1}} & 0& -\frac{c_{1}+c_{2}}{m_{1}} & \frac{c_{2}}{m_{1}} & 0\\ \frac{k_{2}}{m_{2}} & -\frac{k_{2}+k_{3}}{m_{2}} & \frac{k_{3}}{m_{2}} & \frac{c_{2}}{m_{2}}& -\frac{c_{2}+c_{3}}{m_{2}} & \frac{c_{3}}{m_{2}} \\ 0& \frac{k_{3}}{m_{3}} & -\frac{k_{3}}{m_{3}} & 0& \frac{c_{3}}{m_{3}} & -\frac{c_{3}}{m_{3}} \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \dot{x}_{1}\\ \dot{x}_{2}\\ \dot{x}_{3} \end{bmatrix}+ \begin{bmatrix} 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ \frac{1}{m_{1}} & 0& 0\\ 0& \frac{1}{m_{2}} & 0\\ 0& 0& \frac{1}{m_{3}} \end{bmatrix} \begin{bmatrix} u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}\\ y=\begin{bmatrix} 0& 0& 0& 0& 1& 0 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \dot{x}_{1}\\ \dot{x}_{2}\\ \dot{x}_{3} \end{bmatrix} \end{matrix}\right.$$

# 三、matlab 程序编写

在 matlab 程序编写中，直接编写 A、B 两个矩阵过复杂，可以建立中间变量来进行状态空间矩阵的编写，记

$$\begin{array}{c} M=\begin{bmatrix} m_{1}& 0& 0\\ 0& m_{2}& 0\\ 0& 0& m_{3} \end{bmatrix}\\ C=\begin{bmatrix} c_{1}+c_{2}& -c_{2}& 0\\ -c_{2}& c_{2}+c_{3}& -c_{3}\\ 0& -c_{3}& c_{3} \end{bmatrix}\\ K=\begin{bmatrix} k_{1}+k_{2}& -k_{2}& 0\\ -k_{2}& k_{2}+k_{3}& -k_{3}\\ 0& -k_{3}& k_{3} \end{bmatrix} \end{array}$$

则矩阵 A、B 可记为

$$\begin{array}{c} A=\begin{bmatrix} 0& I\\ -M^{-1}K& -M^{-1}C \end{bmatrix}\\ B=\begin{bmatrix} 0\\ M^{-1} \end{bmatrix} \end{array}$$