# 一、正定矩阵与椭圆的关系

二维空间中椭圆最基本的形式为

$$\frac{x^{2}}{a^{2}} +\frac{y^{2}}{b^{2}} =1$$

上面的这个方程写成矩阵的形式为

$$\begin{bmatrix} x\\ y \end{bmatrix}^{T} \begin{bmatrix} \frac{1}{a^{2}} & 0\\ 0& \frac{1}{b^{2}} \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} =x^{T}Ax=1$$

$A$ 的特征值为

$$\lambda _{1}=\frac{1}{a^{2}},\space \lambda _{2}=\frac{1}{b^{2}}$$

$A$ 的归一化特征向量为

$$\mu _{1}=\begin{bmatrix} \frac{1}{\sqrt{2} }\\ 0 \end{bmatrix},\space \mu _{2}=\begin{bmatrix} 0\\ \frac{1}{\sqrt{2} } \end{bmatrix}$$

椭圆的长短轴分别沿着矩阵$A$ 的两个特征向量的方向，而两个与之对应的特征值分别是半长轴和半短轴的长度的平方的倒数，即满足

$$a=\frac{1}{\sqrt{\lambda_{1} }},\space b=\frac{1}{\sqrt{\lambda_{2} }}$$

更一般的，对于如下方程所示椭圆

$$ax^{2}+2bxy+cy^{2}=1$$

化为矩阵形式是

$$\begin{bmatrix} x\\ y \end{bmatrix}^{T} \begin{bmatrix} a & b\\ b & c \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} =x^{T}Ax=1$$

# 二、椭圆的一般方程

椭圆的一般方程为

$$\frac{\left [\left (x-x_{0} \right ) \cos \theta +\left (y-y_{0} \right )\sin \theta \right ]^{2}}{a^{2}} +\frac{\left [\left (x-x_{0} \right )\sin \theta -\left (y-y_{0} \right )\cos \theta \right ]^{2}}{b^{2}} =1$$

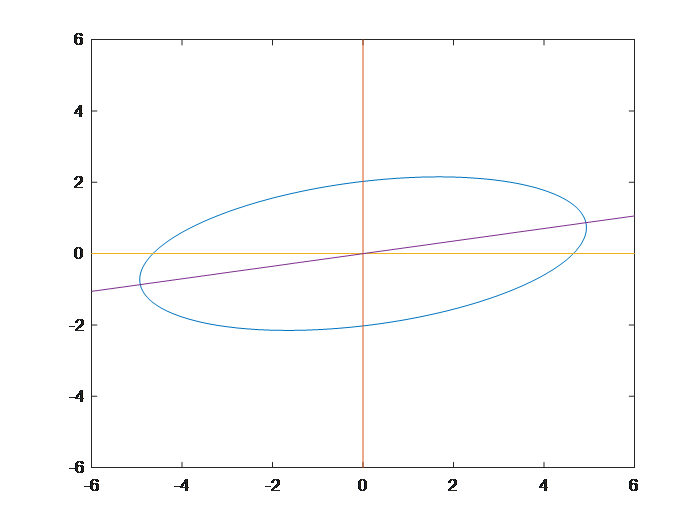
其中 $(x_{0},y_{0})$ 为椭圆中心点，θ 为椭圆倾角，椭圆倾角如下图紫色线与黄色线所成锐角

将该椭圆变为矩阵形式为

$$\begin{bmatrix} x-x_{0}\\ y-y_{0} \end{bmatrix}^{T} \begin{bmatrix} \frac{\cos ^{2}\theta}{a^{2}}+\frac{\sin ^{2}\theta}{b^{2}} & \frac{\cos\theta\sin\theta}{a^{2}}+\frac{\cos\theta\sin\theta}{b^{2}}\\ \frac{\cos\theta\sin\theta}{a^{2}}+\frac{\cos\theta\sin\theta}{b^{2}} & \frac{\sin ^{2}\theta}{a^{2}}+\frac{\cos ^{2}\theta}{b^{2}} \end{bmatrix} \begin{bmatrix} x-x_{0}\\ y-y_{0} \end{bmatrix}=1$$

# 三、绘制一般椭圆的 matlab 程序

ellipse_l = 5;  % 椭圆半长轴

ellipse_s = 2;  % 椭圆半短轴

ellipse_theta = (10) / 180 * pi;   % 椭圆倾角

ellipse_center = [5, 4.5];  % 椭圆中心点坐标

cut_off_value = 3;  % 奇异值截断值

% 椭圆展开后方程的各个参数

a = ellipse_l^2*sin (ellipse_theta)^2+ellipse_s^2*cos (ellipse_theta)^2;

b = 2*(ellipse_s^2-ellipse_l^2)*sin (ellipse_theta)*cos (ellipse_theta);

c = ellipse_l^2*cos (ellipse_theta)^2+ellipse_s^2*sin (ellipse_theta)^2;

d = -ellipse_l^2*ellipse_s^2;

% 绘制椭圆图像

figure (1)

fimplicit (@(x,y) a.*(x-ellipse_center (1)).^2+b.*(x-ellipse_center (1)).*(y-ellipse_center (2))+c.*(y-ellipse_center (2)).^2+d,[0 10 0 10]);

hold on

scatter (ellipse_center (1),ellipse_center (2))

hold on