首页 最优化

# 一、最近邻搜索 (Nearest neighbor search, NNS)

最近邻搜索算法是为 TSP 编程的最简单的贪婪方法之一。
注：贪婪算法是指在对问题求解时，总是做出在当前看来时最好的选择，也就是说不从整体最优上加以考虑，算法得到的时在某种意义上的局部最优解
NNS 算法的流程为：
1、首先固定起点城市，并将起点城市当作当前目标城市
2、在剩余未被选取的城市中选取距离当前目标城市最近的城市作为下一个目标城市
3、重复步骤 2 直到所有城市都被依次选取完毕
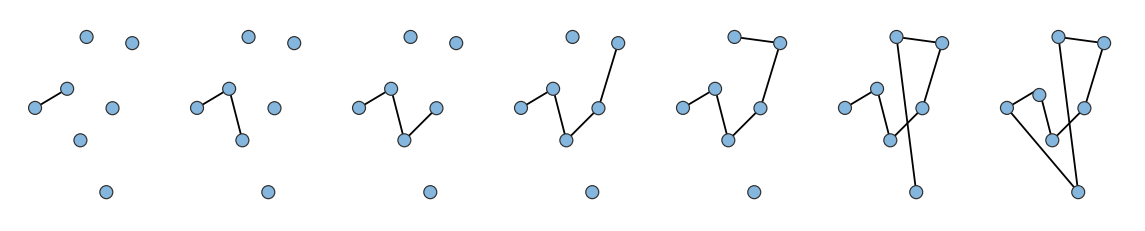
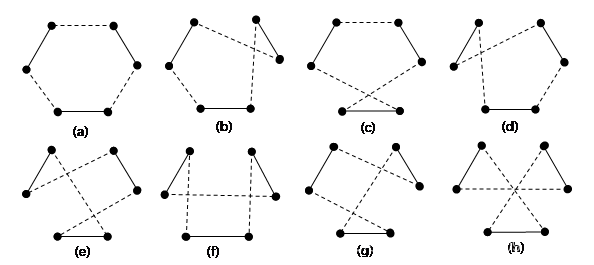
最近邻搜索的过程图如下图所示

# 二、试验方法 (Pilot Method)

课本介绍：
  试验方法列举了通过在初始解中加入一个元素可以得到的所有部分解。然后将引导启发式应用于所有这些部分解，以得到尽可能多的完整解。在最佳完全解的起点的部分解被用作新的起始解，直到没有更多的东西要添加。试验方法的框架需要一个所谓的试点试探法，以完全完成部分解决方案。
自我理解：
  试验方法的核心思想是基于当前部分解（不完整的解），在每一次迭代的过程中添加不属于当前部分解的元素构成更加完整的下一代部分解集（所有可添加元素添加后的集合），通过其它搜索算法（如最近邻法、2opt 等）将部分解集扩展称为可执行解集，选择目标值最大（或最小）的可执行解对应添加的元素作为插入元素，从而得到下一代更加完整的部分解，重复该过程直到没有元素可以插入（即得到一个完整的解）。
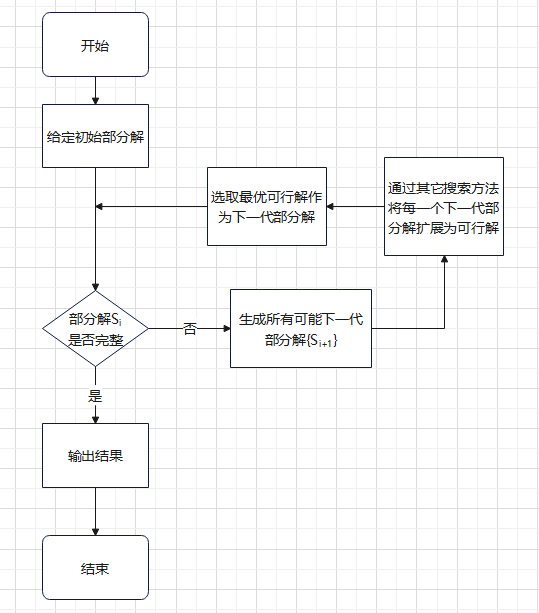
试验方法流程图如下图所示

# 三、最佳改进启发式

课本介绍：
  使用最佳改进策略，在每次迭代时彻底检查邻域。所识别的最佳邻居解是用于后续迭代的当前解。
自我理解：
  最佳改进策略是一种搜索策略，并不代表一种具体的搜索方法。这种策略可以基于其它具体搜索方法（如 2opt 等），在每次迭代中先找到当前解的所有邻域解，以最优邻域解作为下一代的解，直到当前邻域中没有任何一个邻域解优于当前解，则搜索结束。
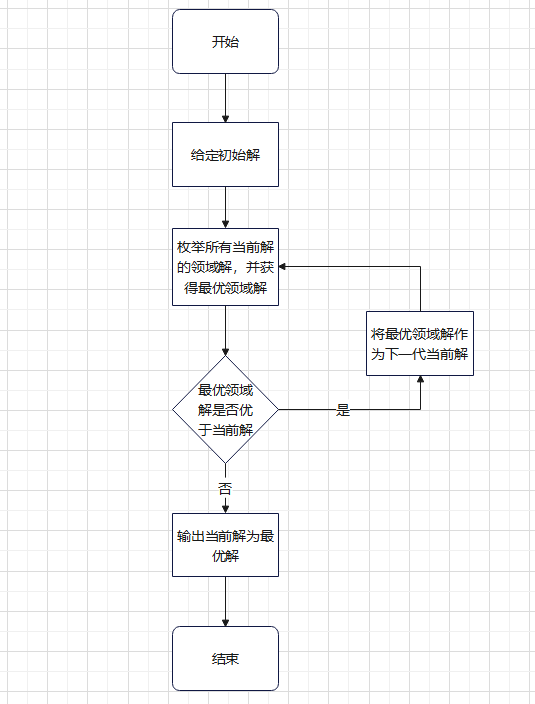
改进启发式搜索算法流程图如下图所示

# 四、3-opt

  3-opt 算法是一种针对 TSP 问题的局部搜索算法，通过选取路径中不相邻的三个节点之间的连接删除，然后尝试其它 7 种不同的连接方式，并计算不同连接方式之后的路径长度，选取路径长度最短的连接方式作为新的连接方式，对于路径中不同的三个连接重复此过程，直到所有的三个连接都没有新的连接方式。3-opt 示意图如下图所示

# 五、模拟退火算法 (SA)

  模拟退火法是最早的局部搜索技术之一，它在每次迭代时并不严格地提高解的质量。模拟退火算法的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在求解空间中随机寻找目标函数的全局最优解，即在陷入局部最优解时能概率性地跳出并最终趋于全局最优。
  在了解模拟退火算法之前，首先要了解 Metropolis 准则。Metropolis 准则定义了系统由当前状态变为下一状态的接受概率，当下一状态小于当前状态时，接收改状态，否则按照一定概率来接受该状态。Metropolis 准则的公式如下：

p={1,E(n+1)<E(n)exp(−E(n+1)−E(n)T),E(n+1)≥E(n)p=\left\{\begin{matrix} 1, & E(n+1)<E(n)\\ exp(-\frac{E(n+1)-E(n)}{T} ), & E(n+1)\ge E(n) \end{matrix}\right.

算法的流程如下
（1）初始温度T0T_0，令T=T0T=T_0，随机产生一个初始解x0x_0，并计算其对应的目标函数值E(x0)E(x_0)
（2）令T=λTT=λT 或T=T1+λT T=\frac{T}{1+\lambda T} \space，其中λλ 取值00 到11 之间，为温度下降速度的参数
（3）对当前解xtx_t 施加随机扰动，在其邻域内产生一个新解xt+1 x_{t+1}\space，并计算对应的目标函数值E(xt+1)E(x_{t+1})，计算△E=E(xt+1)−E(xt)\bigtriangleup E=E(x_{t+1})-E(x_t)
（4）按照 Metropoils 准则判断是否接受新解
（5）重复 L 次扰动和接受过程，即执行步骤 3 和 4，直到温度 T 小于终止温度
算法流程图如下

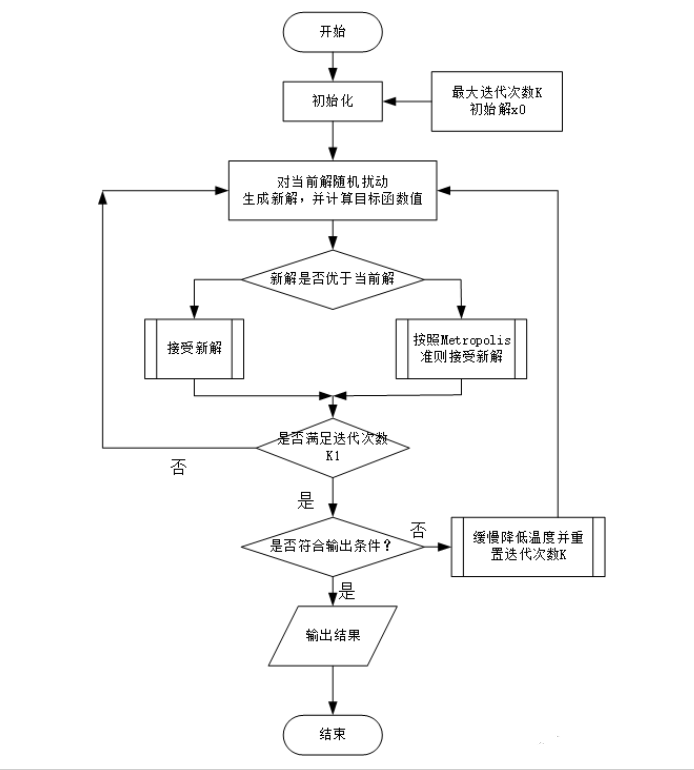
# 六、噪声方法

  噪声方法的参数是用迭代次数设置的概率分布，在每次评估解时，都会生成随机噪声事件，一般来说，它的期望值为 0，它的方差随着迭代次数的增加而减小，噪声等级分布与迭代次数的关系如下图所示

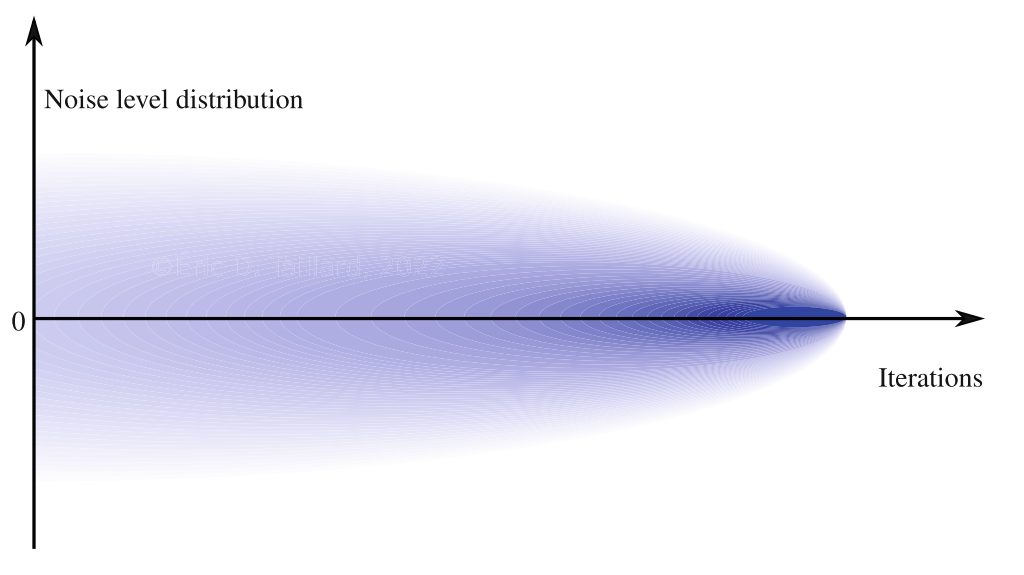
  噪声方法的伪代码如下所示

# 七、变邻域搜索 (VNS)

  变邻域搜索算法（Variable Neighborhood Search）属于一种局部搜索算法，是指通过改变邻域结构来达到搜索到最优解的过程。
  VNS 基于以下两个事实：
  1、一个邻域结构的局部最优解不一定是另一个邻域结构的局部最优解
  2、全局最优解是所有可能邻域的局部最优解
  变邻域搜索的伪代码如下所示

# 八、贪婪随即自适应搜索算法 (GRASP)

  贪婪随机自适应搜索过程通过局部搜索反复改进用贪婪构造方法获得的解。该方法包括两个参数 Imax（算法外循环的重复次数）和 α（用于调整随机化程度）。
  GRASP 是针对组合优化问题的多起点元启发式方法，其中每个迭代基本上都包含两个阶段，即：
  (1) 构造阶段 construction
  (2) 局部搜索阶段 improvement
  构造阶段构造了一个可接受的解。在局部搜索阶段，GRASP 剖析这个解的邻域，更新解，直到解达到局部最优。更直白的说，GRASP 首先从问题的组成元素中构造一个解（在构造阶段），然后再 “调整” 这个解决方案（在局部搜索阶段）。

# 九、Lin-Kernighan 算法 (LK)

  Lin-Kernighan 算法（又称 λ-opt 算法）属于局部优化算法类中的一种，这是因为该算法通过交换边来局部改善现有旅行，被交换的边是通过随机选取的，交换过程持续下去，直到不能再获得更优的解为止。Lin-Kernighan 算法基于 λ- 最优性原理。
  λ- 最优性原理：如果用任意 λ 条新边取代任意 λ 条现有边获得的新解都不及现有解的成本低，那么现有解满足 λ- 最优（或简记为 λ-opt）。
  λ 值被预先确定也有不好的一面，这样做将无法通过改变 λ，使算法的运行时间和求解质量获得较好的协调。Lin 和 Kernighan 通过引入了一种称作可变 λ-opt 的启发式算子解决了该问题。他们的算法再执行期间动态改变 λ 值。在每一次迭代中，算法都要根据先前运算历史决定是否给目前的 λ 值一个增量，进而通过该 λ 交换获得成本更小的旅行。
Lin-Kernighan 算法的原理为：
（1）对当前基进行邻域搜索
（2）在邻域中搜索到比最优解更优的解时立刻替代最优解，并以最优解作为基，返回（1）
（3）如果没有优于最优解的邻域解，那么尝试寻找邻域中第二指标优于最优解的邻域解（同时也是邻域中第二指标最优，需遍历完所有邻域），并以第二指标最优解作为基，返回（1）
（4）如果没有第二指标优于最优解的邻域解，则结束
Lin-Kernighan 算法的流程图如下所示

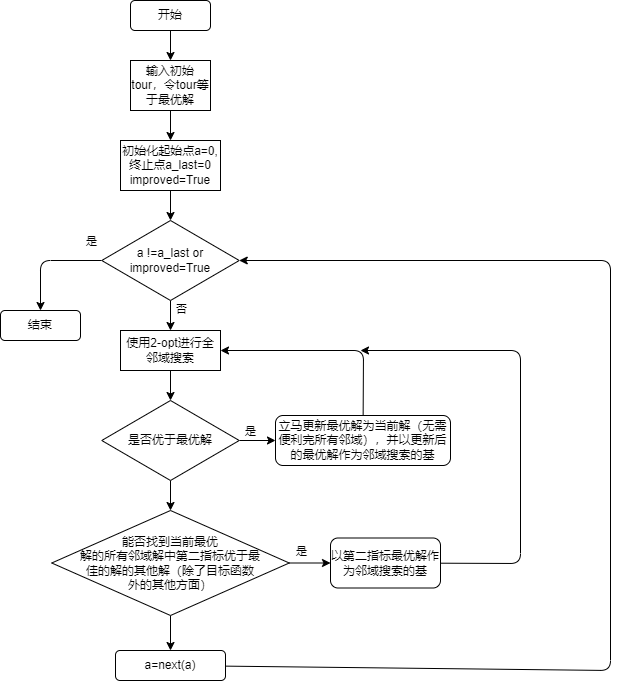
# 十、快速蚁群算法（FANT）

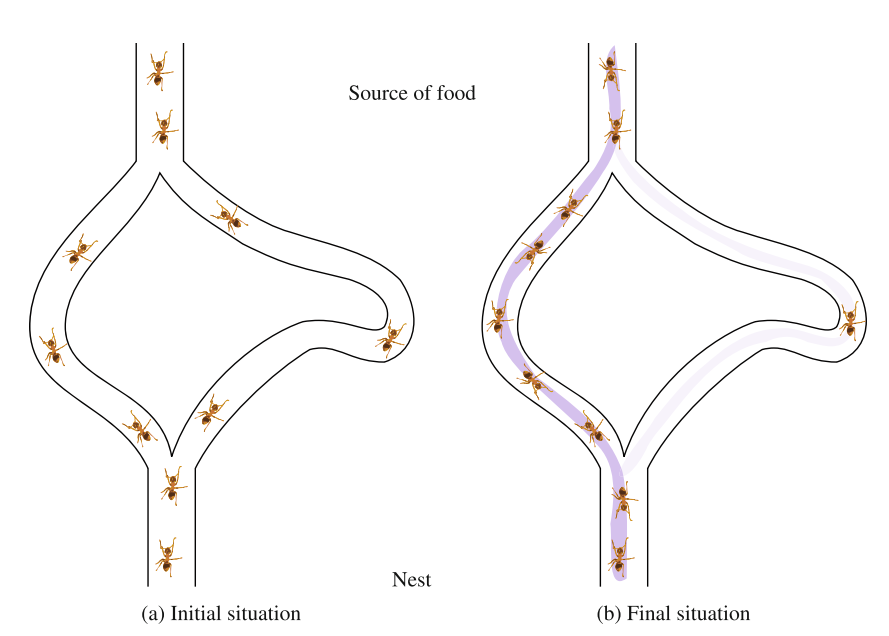
  下图展示了一只蚂蚁的典型行为，这是一个真实的被隔离的蚁群的经历。后者只能通过一个孔来寻找食物。最后一个连接到一个管子上，这管子分成两个分支，再进一步连接。左边的树枝比右边的短。由于蚂蚁一开始没有这方面的信息，所以蚂蚁在两个分支中平均分布（图 a）。
  在探索过程中，每只蚂蚁都会掉落一种化学物质，它们的触角很容易探测到这种物质，这将有助于它们返回蚁巢。这种携带信息的化学物质叫做信息素。在返回的路上，一只蚂蚁会根据食物来源的质量储存大量的信息素。自然地，一只发现了一条短路径的蚂蚁能够比那些使用坏路径的蚂蚁更早返回。
  因此，沉积在最短路径上的信息素的数量增长更快。因此，新来的蚂蚁有了选择路径的信息，并倾向于选择最短的树枝。一段时间后，观察到几乎所有的蚂蚁都使用最短的树枝 (图 b)。因此，蜂群共同决定一个最优路径，而每个个体只看到自己天线的顶端。

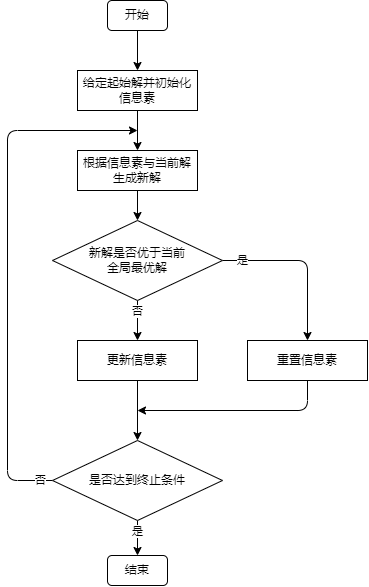
快速蚁群算法流程图如下所示（根据代码进行理解，部分理解不到位）

# 十一、禁忌搜索算法（TS）

  禁忌搜索（Tabu search）的关键思想是用超越局部最优的局部搜索来探索解空间。这意味着设计一种机制来防止循环现象，即进入一个循环，在这个循环中，有限的解子集被反复访问。最简单的概念是记住在局部搜索中连续遇到的所有解，但防止后者选择已经访问过的邻居解。被访问的解决方案因此成为禁忌。
  一般 TS 的伪代码如下

# 禁忌搜索的持续时间

  零禁忌时间与随机搜索毫无差别，禁忌搜索持续时间过长会导致搜索效率低下并易陷入循环。一种选择较低的禁忌持续时间同时又能有效防止循环现象的技术是在每次迭代中随机设置它，一个经典的方法是在最小持续时间 dmin 和最大值 dmax = dmin +Δ 之间随机选择禁忌持续时间。

# 破禁准则

  无条件禁止移动可能会导致搜索效率的低下。例如，在某些情况下会跳过对找到的最佳解决方案的改进。因此，如果移动 m 允许获得一个比当前全局最优解更好的解，则可无视禁忌来保留它，这种规则即为破禁准则。

# 长期记忆

  短时间记忆的禁忌搜索的一个缺点是它只能做出很小的改变。可将长期记忆与短期记忆相结合，从而克服这一缺点。长期记忆可以通过很多种方式来表现，如持续统计每次解的移动。

# 最终流程图

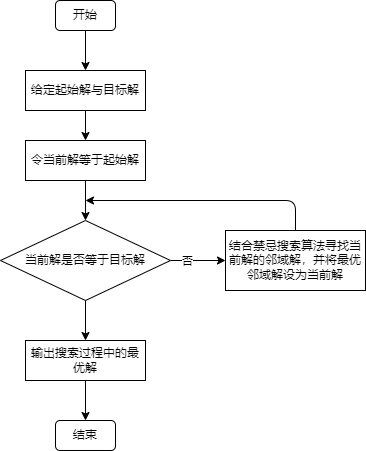
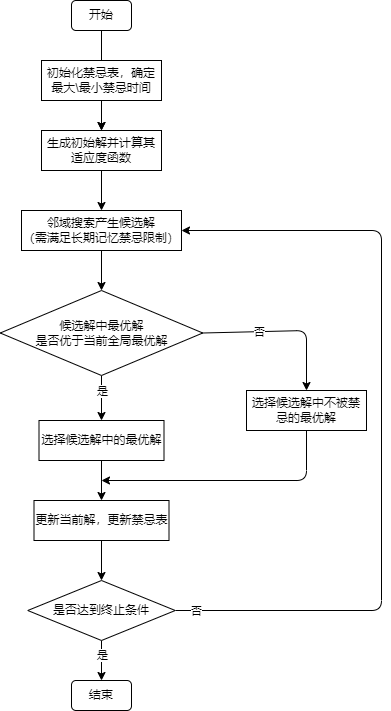
将禁忌搜索和以上内容相结合后的流程图为

# 十二、模因算法（GA）

  遗传算法有两个主要缺点：首先，没有任何东西能保证找到的最佳解决方案不能通过简单的局部修改得到改进。其次，种群的多样性随着世代循环的每次迭代而下降，最终只包含同一个体的克隆。
  模因算法（Memetic Algorithms）通过在生成子代后应用局部搜索来解决第一个缺点（如 LK 算法，2-opt 算法等）。第二个缺点的解决方法是立即消除重复解。（也是和遗传算法的区别）

# 十三、带路径重链接的贪婪随即自适应搜索算法（GRASP-PR）

  GRASP-PR（greedy adaptive search procedure with path relinking）是一种使用元启发式的核心组件（构造，局部搜索和解决方案集合的管理）且输入参数较为简单的方法。
  路径重链接（PR）通过选择两个解决方案，从初始解寻找最优邻域解直至搜索到目标解，在此过程中生成的最优解即为 PR 得到的最优解。
  GRASP-PR 的伪代码如下

GRASP-PR 的流程图如下

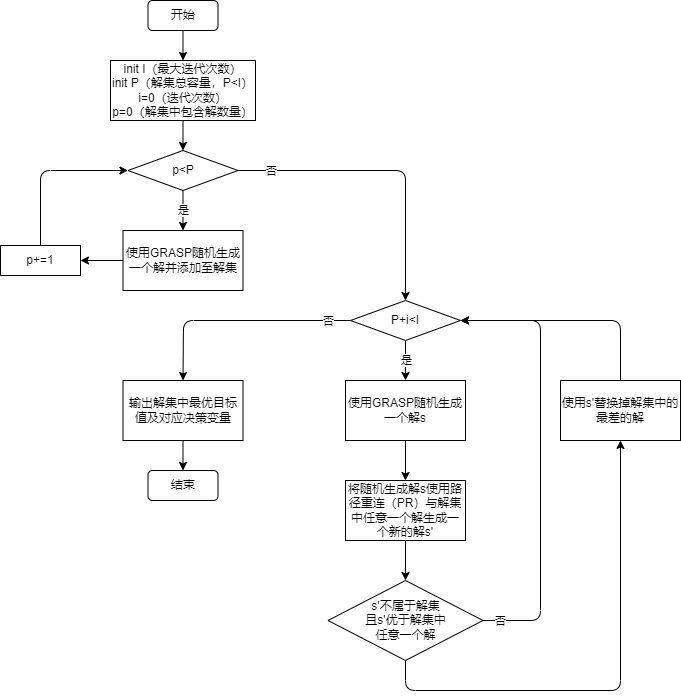
PR 的流程图如下

更新于 阅读次数 次