首页 最优化

# 前言：Pareto 最优解定义

  多目标优化问题与单目标优化问题有很大差异。当只有一个目标函数时，人们寻找最好的解，这个解优于其他所有解，通常是全局最大或最小，即全局最优解。
  而当存在多个目标时，由于目标之间存在冲突无法比较，所以很难找到一个解使得所有的目标函数同时最优，也就是说，一个解可能对于某个目标函数是最好的，但对于其他的目标函数却不是最好的，甚至是最差的。
  因此，对于多目标优化问题，通常存在一个解集，这些解之间就全体目标函数而言是无法比较优劣的，其特点是：无法在改进任何目标函数的同时不削弱至少一个其他目标函数。这种解称作非支配解（ nondominated soluitons ）或 Pareto 最优解（ Pareto optimal Soluitons ），其定义如下：

  对于最小化多目标问题，nn 个目标分量fi(i=1,⋯ ,n)f_{i}(i=1, \cdots, n) 组成的向量

f(Xˉ)=(f1(Xˉ),f2(Xˉ),⋯ ,fn(Xˉ))f(\bar{X})=\left(f_{1}(\bar{X}), f_{2}(\bar{X}), \cdots, f_{n}(\bar{X})\right)

  Xˉu∈U\bar{X}_{u} \in U 为决策变量，若Xˉu\bar{X}_{u} 为 Pareto 最优解，当且仅当不存在决策变量Xˉν∈U\bar{X}_{\nu} \in U，v=f(Xˉv)v=f\left(\bar{X}_{v}\right) 支配u=f(Xˉu)u=f\left(\bar{X}_{u}\right)，即不存在Xˉ∈U\bar{X} \in U，使得下式成立：

∀i∈{1,⋯ ,n},fi(Xˉv)≤fi(Xˉu)\forall i \in\{1, \cdots, n\}, f_{i}(\bar{X}_{v} ) \leq f_{i} (\bar{X}_{u})

# 一、非支配排序遗传算法（NSGA）

  （百度解释） NSGA 与简单的遗传算法的主要区别在于：该算法在选择算子执行之前根据个体之间的支配关系进行了分层。其选择算子、交叉算子和变异算子与简单遗传算法没有区别。
  （自我理解）在多目标优化问题中，个体解之间无法直接比较优劣，故无法像单目标算法一样基于适应度值进行选择操作，从而需要在选择操作之前进行一些其他操作，而在选择操作之前的操作即为 NSGA 算法与传统遗传算法的不同之处。

# 1.1 非支配排序算法

  非支配排序算法的目标是将种群中的个体根据支配关系进行分层，考虑一个目标函数个数为 K(K>1) 、规模大小为 N 的种群，通过非支配排序算法可以对该种群进行分层，具体的步骤如下：

（1）设 j=1；
（2）对于所有的g=1,2,…,Ng=1,2, \ldots, N 且g≠jg \neq j，基于适应度函数比较个体xjx^j 和个体xgx^g 之间的支配与非支配关系；
（3）如果不存在任何一个个体xgx^g 优于xjx^j，则xjx^j 标记为非支配个体；
（4）令 j=j+1，转到步骤（1），直到找到所有的非支配个体。

  通过上述步骤即可将整个种群根据个体的支配关系进行分层。

# 1.2 虚拟适应度值

  在对种群进行非支配排序的过程中，需要给每一个非支配层指定一个虚拟适应度值。级数越大，虚拟适应度值越小；反之，虚拟适应度值越大。这样可以保证在选择操作中等级较低的非支配个体有更多的机会被选择进入下一代，使得算法以最快的速度收敛于最优区域。
  比如指定第一层个体的虚拟适应度值为 1 ，第二层个体的虚拟适应度值应该相应减少，可取为 0.9 ，依此类推。

# 1.3 拥挤策略的小生境（NIChe）技术

  另一方面，为了得到分布均匀的 Pareto 最优解集，就要保证当前非支配层上的个体具有多样性。 NSGA 中引入了基于拥挤策略的小生境 ( NIChe ) 技术，即通过适应度共享函数的方法对原先指定的虚拟适应度值进行重新指定。算法如下所示：

  假设第mm 级非支配层上有nmn_m 个个体，每个个体的虚拟适应度值为fmf_m，且令i,j=1,2,⋯ ,nmi,j=1,2,\cdots,{n}_{m}，则具体的实现步骤如下：
（1）计算出属于一个非支配曾的个体ii 和个体jj 的欧几里得距离：

d(i,j)=∑l=1L(xli−xljxlμ−xld)2d(i, j)=\sqrt{\sum_{l=1}^{L}\left(\frac{x_{l}^{i}-x_{l}^{j}}{x_{l}^{\mu}-x_{l}^{d}}\right)^{2}}

  其中，L 为问题空间的变量个数，xlμx_{l}^{\mu}、xldx_{l}^{d} 分别为xlx_{l} 的上、下界。
（2）共享函数ss 表示个体xix^i 和小生境群体中其他个体的关系：

s(d(i,j))={1−(d(i,j)σshare )αd(i,j)<σshare 0 else s(d(i, j))=\left\{\begin{array}{lc} 1-\left(\frac{d(i, j)}{\sigma_{\text {share }}}\right)^{\alpha} & d(i, j)<\sigma_{\text {share }} \\ 0 & \text { else } \end{array}\right.

  其中σshare\sigma_{\text {share}} 为共享半径，α\alpha 为常数。
（3）j=j+1j=j+1，如果j≤nmj\le {n}_{m}，则转到步骤（1），否则计算出个体xix^i 的小生境数量为：

ci=∑j=1nms(d(i,j))c_{i}=\sum_{j=1}^{n_{m}} s(d(i, j))

（4）计算出个体xix^i 的共享适应度值：

fm′(i)=fm(i)cif_{m}^{\prime}(i)=\frac{f_{m}(i)}{c_{i}}

反复执行以上的步骤（1）→（4）可以得到每一个个体的共享适应度值。

# 二、带精英策略的非支配排序的遗传算法（NSGA-II）

   NSGA 算法比传统的多目标遗传算法效果更好。但是在实际应用中发现 NSGA 算法仍具有一定的缺点，主要体现在以下方面：

（1）算法计算量大。 NSGA 算法的计算复杂度与种群数量NN、目标函数个数mm 的关系为T=O(mN3)T=O(mN^3)，当种群规模较大、目标函数较多时所耗时间较长；
（2）没有应用精英策略。未通过精英策略提高优秀个体的保留概率，因而无法加快程序的执行速度；
（3）需要人为地指定共享半径σshareσ_{share}，对于经验的要求非常高。

  为了改善 NSGA 算法的缺点， Deb 等人在 2002 年提出了 NSGA-II 算法。相对于 NSGA 算法， NSGA-II 算法主要在以下三个方面做了改进：

（1） NSGA-II 算法使用了快速非支配排序法，将算法的计算复杂度由O(mN3)O(mN^3) 降到了O(mN2)O(mN^2)，使得算法的计算时间大大减少；
（2）用拥挤度的方法代替了需指定共享半径的适应度共享策略，并作为在同级个体中选择优秀个体的标准，保证了种群中个体的多样性，有利于个体能够在整个区间内进行选择、交叉和变异；
（3）采用了精英策略，将父代个体与子代个体合并后进行非支配排序，使得搜索空间变大，生成下一代父代种群时按顺序将优先级较高的个体选入，并在同级个体中采用拥挤度进行选择，保证了优秀个体能够有更大的概率被保留。

# 2.1 整体流程

  首先，随机产生规模为NN 的初始种群，非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；
  其次，从第二代开始， 将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群：依此类推，直到满足程序结束的条件。

# 2.2 精英策略

   NSGA-II 算法引入了精英策略，达到保留优秀个体淘汰劣等个体的目的。精英策略通过将父代与子代个体混合形成新的群体，扩大了产生下一代个体时的筛选范围。以图所示的例子进行分析：

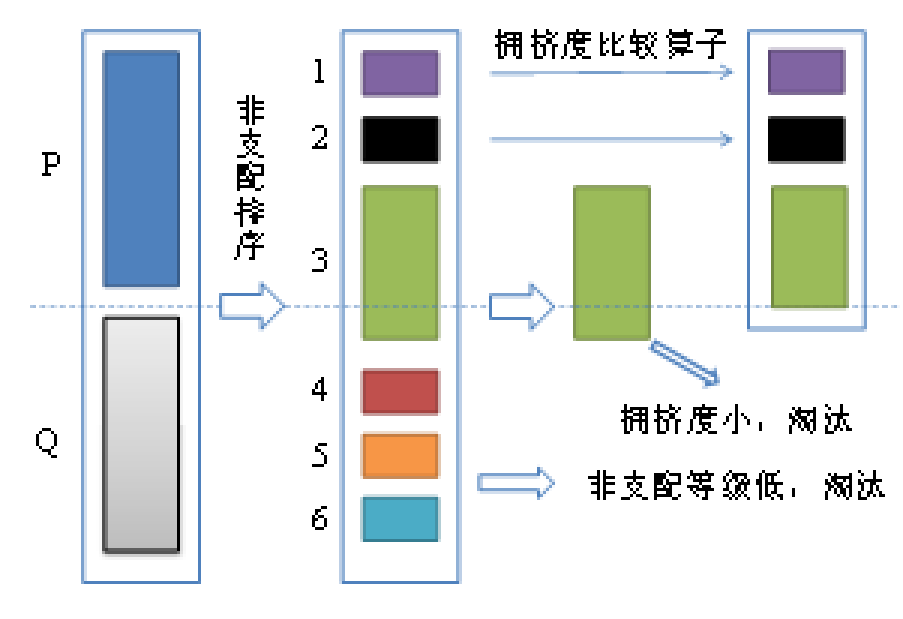
  上图中PP 表示父代种群，设其中的个体数量为nn，QQ 表示子代种群，图示具体步骤如下：

（1）将父代种群和子代种群合并形成新的种群。之后对新种群进行快速非支配排序（2.3 中介绍），本例中将种群分成了66 个 Pareto 等级。
（2）进行新的父代的生成工作，先将 Pareto 等级为11 的非支配个体放入新的父代集合当中，之后将 Pareto 等级为22 的个体放入新的父代种群中，以此类推。
（3）若等级为kk 的个体全部放入新的父代集合中后，集合中个体的数量小于nn，而等级为k+1k+1 的个体全部放入新的父代集合中后，集合中的个体数量大于nn，则对第k+1k+1 等级的全部个体计算拥挤度并将所有个体按拥挤度进行降序排列（2.4 中介绍）, 之后将等级大于k+1k+1 的个体全部淘汰。本例中可以看出kk 为22，所以对 Pareto 等级为33 的个体计算拥挤度并按其进行降序排序，等级为4 64~6 的个体全部淘汰。
（4）将等级k+1k+1 中的个体按步骤（3）中排好的顺序逐个放入新的父代集合中，直到父代集合中的个体数量等于nn，剩余的个体被淘汰。

# 2.3 快速非支配排序算法（分层）

  假设种群为PP，则该算法需要计算PP 中的每个个体pp 的两个参数npn_p 和SpS_p，其中npn_p 为种群中支配个体pp 的个体数，SpS_p 为种群中被个体pp 支配的个体集合。遍历整个种群，这两个参数的总计算复杂度是O(mN2)O(mN^2)。算法的主要步骤为：

（1）找到种群中所有np=0n_p=0 的个体，并保存在当前集合F1F_1 中；
（2）对于当前集合F1F_1 中的每个个体ii，其所支配的个体集合为SiS_i，遍历SiS_i 中的每个个体ll，执行nl=nl−1n_l=n_l-1，如果nl=0n_l=0，则将个体ll 保存在集合HH 中；
（3）记F1F_1 中得到的个体为第一个非支配层的个体，并以HH 作为当前集合，重复上述操作，直到整个种群被分级。

# 2.4 确定拥挤度和拥挤度比较算子（同一层内分拥挤度）

  在 NSGA 算法中，需要指定共享半径σshareσ_{share}，这对经验要求较高，为了克服这一缺点， NSGA-II 引用了拥挤度和拥挤度比较的概念。

# （1）拥挤度估算

  拥挤度表示空间中个体的密度值，直观上可以用个体周围不包括其他个体的长方形表示，如图所示：

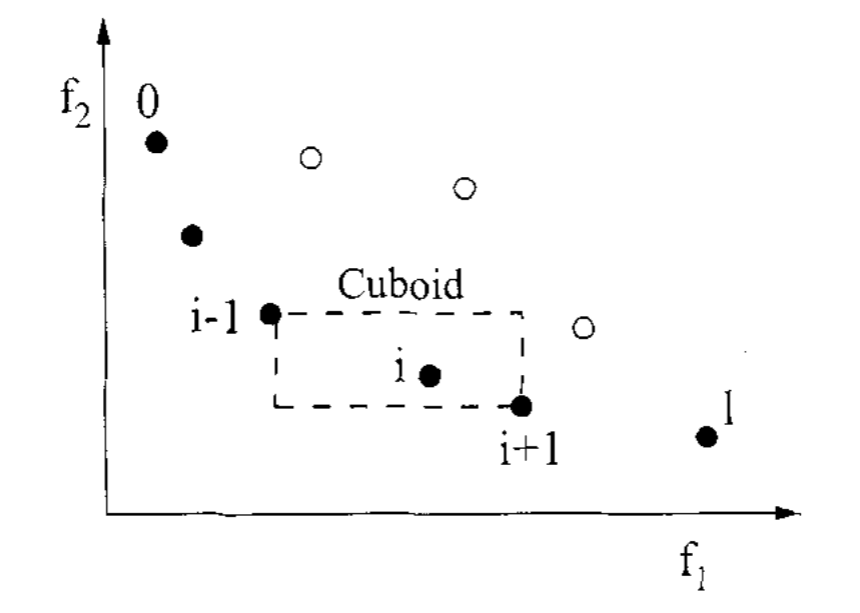
  在计算拥挤距离之前，需要对每个目标函数进行归一化。拥挤距离的计算需要根据每个目标函数值按升序对总体进行排序。然后，对于每个目标函数，边界解 (函数值最小和最大的解) 被分配一个无限距离值。所有其他中间解都被赋一个距离值，等于两个相邻解函数值的归一化绝对值差（自我理解：即上图中的长与宽之和）。对所有目标函数均进行该操作。整体拥挤距离值计算为每个目标对应的个体距离值之和。
  在给集合中的所有种群成员分配了一个距离度量之后，我们可以比较两个解与其他解的接近程度。在某种意义上，一个解的这个距离度量值越小，其他解就越拥挤。这正是我们在下面描述的拥挤比较算子中所比较的。虽然上图给出了两个目标的拥挤距离计算，但该过程同样适用于两个以上目标。

# （2）拥挤度比较算子

  拥挤比较算子 (≺n\prec _n) 引导算法各阶段的选择过程向均匀展开的 pareto 最优前沿方向发展。假设群体中的每个个体都有两个属性：(1) 非支配等级iranki_{rank}；(2) 拥挤度idistancei_{distance}。
  那么我们就可以定义一个拥挤比较算子为：

i≺nj if (iraulk <jrank) or [(irank=jrank) and (idistance >jdistance )]i \prec_{n} j \quad \text { if }\left(i_{\text {raulk }}<j_{\mathrm{rank}}\right)\text { or }\left[\left(i_{\mathrm{rank}}=j_{\mathrm{rank}}\right)\right.\text { and } \left.\left(i_{\text {distance }}>j_{\text {distance }}\right)\right]

  也就是说，在两个非支配等级不同的解决方案之间，我们更喜欢等级较低 (较好) 的解决方案。否则，如果两个解决方案属于同一个前沿，那么我们更倾向于位于较小拥挤区域的解决方案。

# 三、基于参考点的非支配遗传算法（NSGA-III）

   NSGA-III 算法（又称 many-objective NSGA-II ，原始 NSGA-II 为 multiple-objective NSGA-II ）的基本框架与原始 NSGA-II 算法相似，但其选择算子有较大变化。但与 NSGA-II 不同的是， NSGA-II 用拥挤距离对同一非支配等级的个体进行选择， NSGA-III 通过提供和自适应更新大量广泛分布的参考点来维持种群成员间的多样性。

# 3.1 超平面上参考点的确定

# Das and Denni’s 方法

   NSGA-III 是基于参考点的进化算法，因此，我们首先应该知道参考点是如何进行创建的。关于参考点的创建我们这里仅给出创建过程，不给予证明过程，具体详见 Das and Denni’s 文章。关于创建方法， Y. Tian 大神在 《Sampling Reference Points on the Pareto Fronts of Multi-Objective Optimization Problems》 一文中给予了具体的操作步骤，如下：

（1）Let XX be all the (M−1)(M-1)-combinations of {0H,1H,⋯ ,H+M−2H,}\left \{ \frac{0}{H},\frac{1}{H},\cdots, \frac{H+M-2}{H}, \right \};
（2）For each xij∈Xx_{ij} \in X (i.e., the jj-th element of the ii-th combination in XX), xij=xij−j−1Hx_{ij}=x_{ij}-\frac{j-1}{H}；
（3）Let SS be the reference point set, for each sij∈Ss_{ij} \in S and xij∈Xx_{ij} \in X,

{sij=xij−0,j=1sij=xij−xi(j−1),1<j<Msij=1−xi(j−1),j=M\left\{\begin{array}{ll} s_{i j}=x_{i j}-0, & j=1 \\ s_{i j}=x_{i j}-x_{i(j-1)}, & 1<j<M \\ s_{i j}=1-x_{i(j-1)}, & j=M \end{array} \right.

  以H=5H=5，M=3M=3 的例子为例，来解释上述过程
  首先，构造所有M−1=2M-1=2 维x\mathbf{x} 的组合，其中x∈{0H,1H,⋯ ,H+M−2H,}={05,15,25,35,45,55,65,}x \in \left \{ \frac{0}{H},\frac{1}{H},\cdots, \frac{H+M-2}{H}, \right \}=\left \{ \frac{0}{5}, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{5}{5}, \frac{6}{5}, \right \}；
  之后对x∈xx \in \mathbf{x} 进行如下操作并获得新的xij=xij−j−1Hx_{ij}=x_{ij}-\frac{j-1}{H}；
  最后获取每一个参考点的坐标值：

{sij=xij−0,j=1sij=xij−xi(j−1),1<j<Msij=1−xi(j−1),j=M\left\{\begin{array}{ll} s_{i j}=x_{i j}-0, & j=1 \\ s_{i j}=x_{i j}-x_{i(j-1)}, & 1<j<M \\ s_{i j}=1-x_{i(j-1)}, & j=M \end{array} \right.

  下表展示了本例的三个过程：

ii xi1 x_{i1}\space xi2 x_{i2}\space xi1′x_{i1}' xi2′x_{i2}' si1 s_{i1}\space si2 s_{i2}\space si3 s_{i3}\space
1 0 0.2 0 0 0 0 1
2 0 0.4 0 0.2 0 0.2 0.8
3 0 0.6 0 0.4 0 0.4 0.6
4 0 0.8 0 0.6 0 0.6 0.4
5 0 1 0 0.8 0 0.8 0.2
6 0 1.2 0 1 0 1 0
7 0.2 0.4 0.2 0.2 0.2 0 0.8
8 0.2 0.6 0.2 0.4 0.2 0.2 0.6
9 0.2 0.8 0.2 0.6 0.2 0.4 0.4
10 0.2 1 0.2 0.8 0.2 0.6 0.2
11 0.2 1.2 0.2 1 0.2 0.8 0
12 0.4 0.6 0.4 0.4 0.4 0 0.6
13 0.4 0.8 0.4 0.6 0.4 0.2 0.4
14 0.4 1 0.4 0.8 0.4 0.4 0.2
15 0.4 1.2 0.4 1 0.4 0.6 0
16 0.6 0.8 0.6 0.6 0.6 0 0.4
17 0.6 1 0.6 0.8 0.6 0.2 0.2
18 0.6 1.2 0.6 1 0.6 0.4 0
19 0.8 1 0.8 0.8 0.8 0 0.2
20 0.8 1.2 0.8 1 0.8 0.2 0
21 1 1.2 1 1 1 0 0

  如此最终获得的参考点个数为：

refCount⁡=(H+M−1H)=CH+M−1H=CH+M−1M−1\operatorname{refCount}=\left(\begin{array}{c} \mathrm{H}+\mathrm{M}-1 \\ \mathrm{H} \end{array}\right)=\mathrm{C}_{\mathrm{H}+\mathrm{M}-1}^{\mathrm{H}}=\mathrm{C}_{\mathrm{H}+\mathrm{M}-1}^{\mathrm{M}-1}

  参考点分布如下图所示（H=4H=4, M=3M=3，如上述例子参数不同，懒的画了）

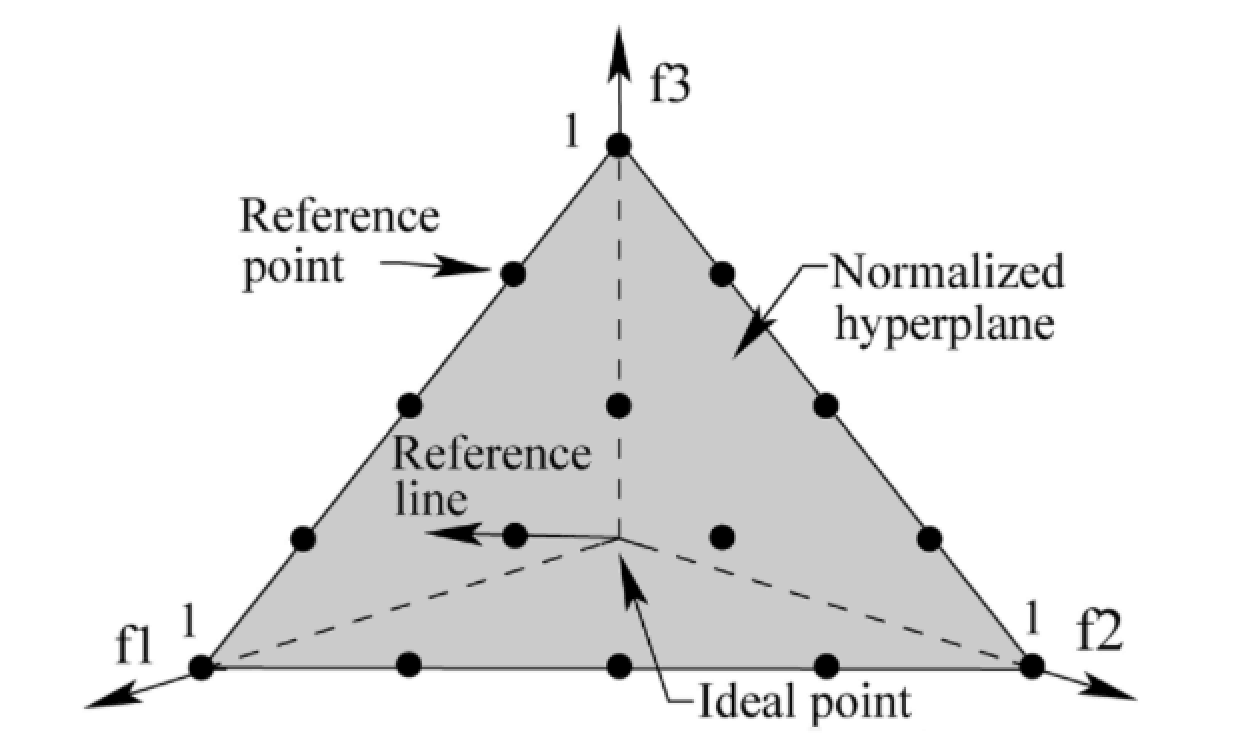
# Deb and Jain’s 方法

  在使用 Das and Denni's 方法，我们可以发现这样创建参考点的方法会出现一个问题。即当H<MH < M 时，将仅会产生 “边界参考点”，即使在H=MH = M 的时候，仅会产生一个 “中间参考点”，如下图所示：

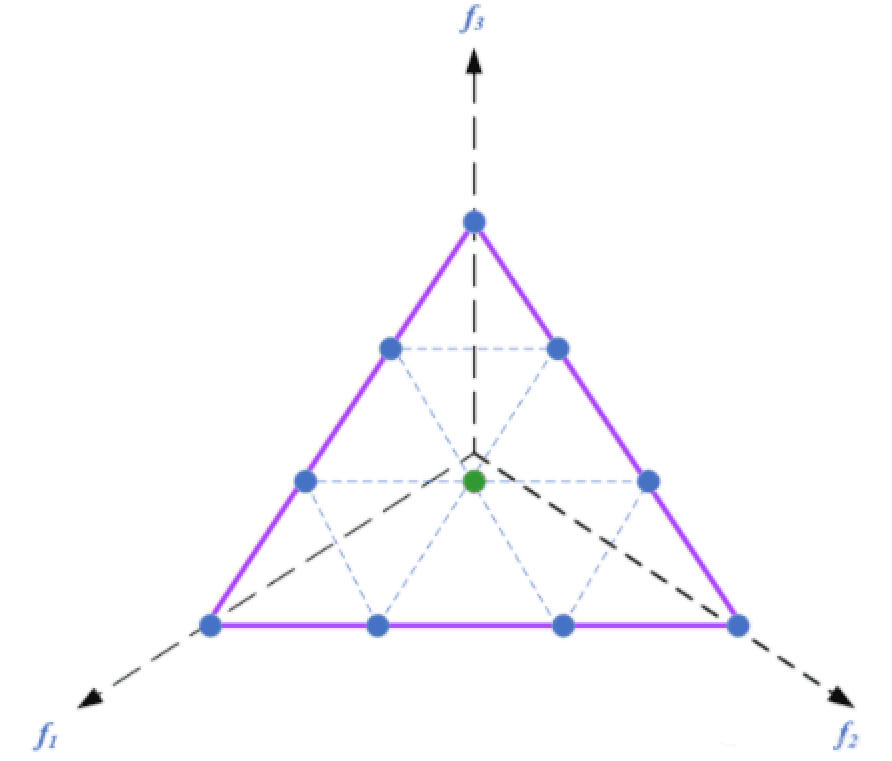
  为了解决这个问题， Deb and Jain's 给出了边界与中间参考点（ boundary and intermediate reference points ）共同构建参考点的方法。其具体操作方法同上述过程，不同点在于中间参考点的坐标值，具体计算过程如下：

（1）Generate S1S_1 by Das and Dennis's method as the point set on boundary layer;
（2）Let S2S_2 be the point set on inside layer, for each sij′∈S2s_{i j}^{\prime} \in S_2 and sij∈S1s_{i j} \in S_1,

sij′=12sij+12Ms_{i j}^{\prime}=\frac{1}{2} s_{i j}+\frac{1}{2 M}

（3）The reference point set S=S1∪S2S=S_{1} \cup S_2.

  注意：1. 中间参考点的计算坐标过程是独立的；2. 参考点总个数为S=S1∪S2S=S_{1} \cup S_2；3. 建议当M≤5\mathrm{M} \leq 5 时，用 Das and Denni's 方法，其它情况用 Deb and Jain's 方法。

# 3.2 自适应归一化

  标准化目标空间的步骤如下所示：

（1）以MM 个最小化目标函数为例，首先得到种群中的所有个体在每一维目标上的最小值，构成当前种群的理想点\text { (z_{1}^{\min}, } \ldots, \text { z_{M}^{\min}) }\space，然后将所有个体的目标值，以及理想点以此理想点为参考作转换操作，这时理想点变为原点，个体的目标值为转换后的临时标准化目标值fi′(x)=fi(x)−ziminf'_{i}(x)=f_{i}(x)-z_{imin}。
（2）然后计算每一维目标轴上的极值点，极值点就是仅在一个目标函数方向比较大，而在其他目标函数方向比较小的点，这MM 个极值点组成了M−1M-1 维的线性超平面。使用 ASF 函数作为目标函数产生极值点的公式如下：

ASF(x,w)=max⁡i=1Mfi′(x)/wi, for x∈StA S F(\mathrm{x}, \mathrm{w})=\max _{i=1}^{M} f_{i}^{\prime}(\mathrm{x}) / w_{i}, \quad \text { for } \mathrm{x} \in S_{t}

  如下引用其他博主以 3 目标为例来描述极值点的产生过程。
  我们初始化种群后，会得到很多个体，他们的目标值可能是 （1，0.4，0.5） ， （2，4，0.8） ， （0.3，0.6，5） 等等，如果有一些点如果在某个目标上的值很大，在另外两个目标上的值很小，则这类点更靠近该目标轴，它们就是所谓的极值点，目标就是找到在一个方向上值很大，另外两个目标值很小的点，但是我们可能得到很多这样的点，这样就需要选择其中最小的作为极值点，所以是一个最小化问题。三个目标的问题话可以找到三个这样的极值点。在 ASF 方程中，固定第一个坐标轴，权重向量 w =（1，10e-6, 10e-6） ，那么 （1，0.4，0.5）/w ，这个时候最大的肯定是 0.5 这个方向，得到值 0.5 x 10e6 。另外两个点同样计算得到： （2，4，0.8） 在 ASF 后变为 0.8 x 10e6 ， （0.3，0.6，5） 在 ASF 后变为 0.6 x 10e6 ，然后选取这三个值中最小的对应的点作为极值点，可知： 0.5 x 10e6 是最小的，对应 （1，0.4，0.5） 是最合适的极值点。
（3）这时可以计算出各个目标方向上的截距aia_i。然后利用截距和临时的标准化目标值计算真正的标准化目标值：

fin(x)=fi′(x)ai−zimin⁡=fi(x)−zimin⁡ai−zimin⁡, for i=1,2,…,Mf_{i}^{n}(\mathrm{x})=\frac{f_{i}^{\prime}(\mathrm{x})}{a_{i}-z_{i}^{\min }}=\frac{f_{i}(\mathrm{x})-z_{i}^{\min }}{a_{i}-z_{i}^{\min }}, \quad \text { for } i=1,2, \ldots, M

  下图展示了对于一个三目标问题，给出了计算截距和由极值点生成超平面的示意图：

# 3.3 个体成员与参考点相关联

  根据目标空间中StS_t 成员的范围自适应归一化每个目标后，需要将每个成员与一个参考点关联起来。为此，通过将参考点与原点连接，我们定义了与超平面上每个参考点对应的参考线。然后，我们计算StS_t 的每个种群成员到每条参考线的垂直距离。在归一化的目标空间中，参考线离成员最近的参考点被认为与总体成员相关联。最后通过个体与参考点关联可以获得每个个体距离最近的参考线以及对应距离，该过程如下所示：

  下图展示了个体成员与参考点关联的示意图：

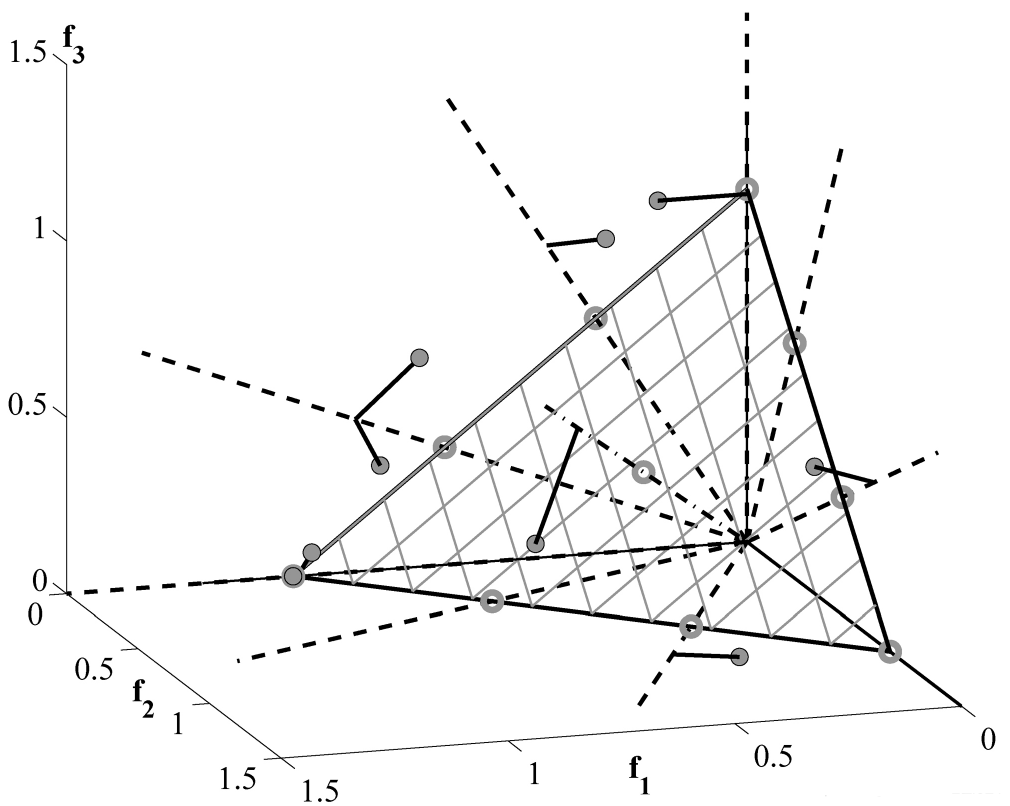
# 3.4 小生境保留（Niche-Preservation）操作

  上边我们构建了种群个体与参考点之间映射关系，获取了每个种群个体距离最小的参考点以及它们之间的距离。前边都是热身工作，接下来，我们正式对最后一前沿种群个体进行操作，筛选最后一前沿种群个体。小生境保留操作的过程如下：

（1）筛选前l−1l-1 层中出现次数较少的参考点集合，然后随机选择其中一个参考点jˉ \bar{j}\space，若在第ll 层个体中存在s:π(s)=j‾,s∈Fl\mathbf{s}: \pi(\mathbf{s})=\overline{\mathrm{j}}, \mathbf{s} \in \mathrm{F}_{l}，则进入步骤（2），否则说明第ll 层个体中不存在这样的个体与参考点对应，故在参考点集合中删掉此参考点以缩小搜索空间。
（2）若第ll 层中存在这样的参考点。如果参考点在前l−1l-1 层以及新加入的个体中出现的次数为00，则选择距离较小的种群个体（之前没有出现过，那么加入距离最短的）；如果参考点在前l−1l-1 层以及新加入的个体中出现的次数不为00，则任意选择该参考点对应的个体。

  该过程的伪代码如下：

更新于 阅读次数 次