首页 最优化

  分解是传统多目标优化的一种基本策略。基于分解的多目标进化算法（ MOEA/D ）将一个多目标优化问题分解为若干个标量优化子问题，并同时对其进行优化。每个子问题仅利用其邻近子问题的信息进行优化，使得 MOEA/D 算法每一代的计算复杂度低于 MOGLS 和非支配排序遗传算法 II （ NSGA-II ）。

# 一、多目标优化问题的分解

# 1.1 加权和方法（Weighted Sum Approach）

  加权和方法中单目标优化函数的表达形式为：

minmize⁡gws(x∣λ)=∑i=1mλifi(x) s.t. x∈Ω\begin{array}{l} \operatorname{minmize} \quad \mathrm{g}^{\mathrm{ws}}(\mathrm{x} \mid \lambda)=\sum_{\mathrm{i}=1}^{\mathrm{m}} \lambda_{\mathrm{i}} \mathrm{f}_{\mathrm{i}}(\mathrm{x}) \\ \text { s.t. } \mathrm{x} \in \Omega \\ \end{array}

  该方法通过一个非负权重向量 λ 将 MOP 转换为单目标子向量。设λ=(λ1,λ2,…λm)T\lambda=\left(\lambda_{1}, \lambda_{2}, \ldots \lambda_{\mathrm{m}}\right)^{\mathrm{T}} 是权重向量且满足∑i=1mλi=1\sum_{\mathrm{i}=1}^{\mathrm{m}} \lambda_{\mathrm{i}}=1（每个目标函数都有自己的权重），那么上述这个单目标优化问题的最优解（唯一）就是一个 Pareto 最优解。
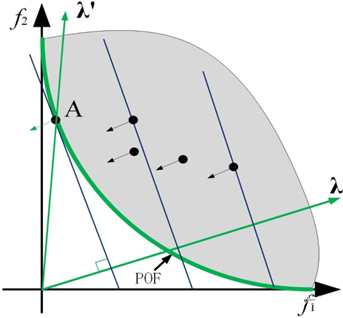
  （自我理解）首先， λ 被称之为权重向量，观察公式，会发现这个公式可以表述为向量 λ={λ1,……,λm} 和每个目标函数值 f(x)={f1(x),……,fm(x)} 的向量点乘，由向量点乘的几何意义可知，由于 λ 的模长为单位长度 1 ，故点乘的结果即为函数值向量在 λ 方向上的投影长度。

  以二目标函数为例，如上图所示，黑色的点为单个解对应的目标函数值点，蓝色的线为等高线，而点乘的结果即为该目标函数值点与原点连线所构成的函数值向量在 λ 方向上的投影长度。在该图中，点 A 对应的解即为在该 λ 构成的单目标函数下的最优解，该解即为原多目标函数的一个 Pareto 解。

# 1.2 切比雪夫聚合法（Tchebycheff Approach）

  切比雪夫法中单目标优化函数的表达形式为：

minimize⁡gte(x∣λ,z∗)=max⁡1≤i≤m{λi(fi(x)−zi∗)} s.t. x∈Ω\begin{aligned} \operatorname{minimize} \quad \mathrm{g}^{\mathrm{te}}\left(\mathrm{x} \mid \lambda, \mathrm{z}^{*}\right)= & \max _{1 \leq \mathrm{i} \leq \mathrm{m}}\left\{\lambda_{\mathrm{i}}\left(\mathrm{f}_{\mathrm{i}}(\mathrm{x})-\mathrm{z}_{\mathrm{i}}^{*}\right)\right\} \\ \text { s.t. } & \mathrm{x} \in \Omega \end{aligned}

  注意该方法中不再含有 Σ 符号，故不能再从向量点乘的角度理解。该方法大致思想是减少最大差距从而将个体逼近 PF （ Pareto Front ）。

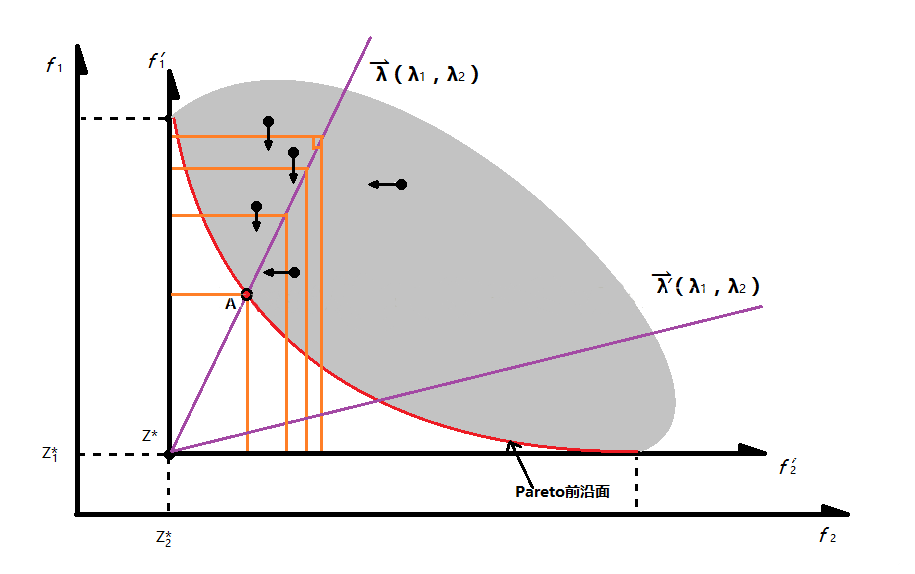
  （自我理解）如上图所示，首先，根据每个函数的最小值，将坐标轴由起始位置移动至每个目标函数的最小值位置。注意该图中横坐标为 f2 ，而纵坐标为 f1 ，而 λ=(λ1, λ2) 。也就是说只要在这条由 λ 构成的蓝色射线之上的解，都有 λ1*f1=λ2*f2 ，由于在目标函数为最大的 λ*f ，故在其中一个目标函数值不变的情况下减少另一个目标函数的值不改变所构成的单目标函数值，从而可知在该方法下的等高线如上图中的橙色线所示。在该图中，点 A 对应的解即为在该 λ 构成的单目标函数下的最优解，该解即为原多目标函数的一个 Pareto 解。

# 1.3 基于惩罚的边界交叉聚合方法（Penalty-based Boundary Intersection (PBI) approach）

# Boundary Intersection (BI) Approach

  该边界交叉聚合方法给出的公式如下：

minimize⁡gbi(x∣λ,z∗)=d subject to z∗−F(x)=dλx∈Ω\begin{aligned} \operatorname{minimize} g^{b i}\left(x \mid \lambda, z^{*}\right) & =d \\ \text { subject to } z^{*}-F(x) & =d \lambda \\ x & \in \Omega \end{aligned}

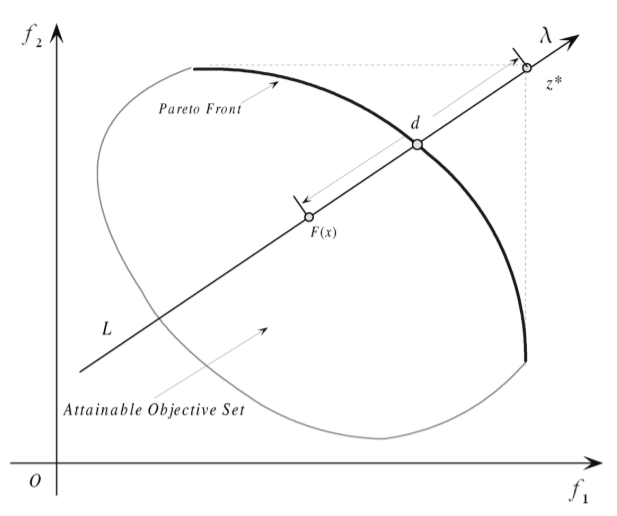
  如下图所示给出了该方法的示意图，其中 λ 为该方向上的单位向量， z* 为各目标函数最大 / 最小值， F(x) 为目标函数值向量，而 d 为构造的单目标函数的优化目标（常量），由于 z*-F(x) 表示从 F(x) 指向 z* 的向量，而 λ 又为预设的单位向量，故 z*-F(x) 必须和 λ 的方向相同，否则无解。故该方法的理解为：在 λ 所构成的射线上寻找最接近 PF 的解，该解即为所构成单目标函数的最优解。

# Penalty-based Boundary Intersection (PBI) approach

  在初始的边界交叉聚合方法中的等式约束不易实现，故添加惩罚因子使单目标搜索的空间可以不局限在单条射线上。基于惩罚的边界交叉聚合方法公式如下：

minimize⁡gbip(x∣λ,z∗)=d1+θd2 subject to x∈Ω\begin{aligned} \operatorname{minimize} & g^{b i p}\left(x \mid \lambda, z^{*}\right)=d_{1}+\theta d_{2} \\ & \text { subject to } x \in \Omega \end{aligned}

d1=∥(z∗−F(x))Tλ∥∥λ∥d_{1}=\frac{\left\|\left(z^{*}-F(x)\right)^{T} \lambda\right\|}{\|\lambda\|}

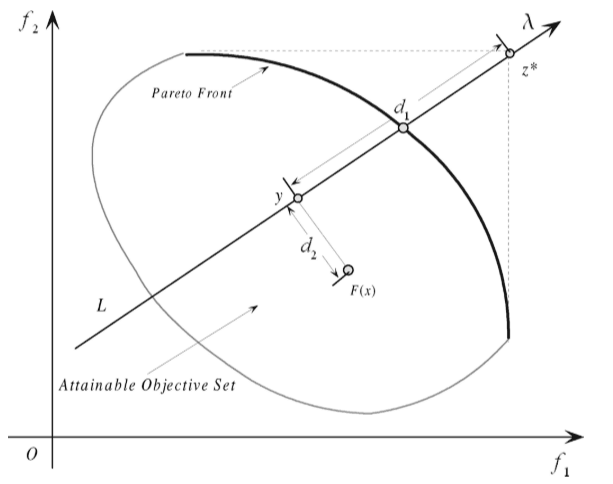
d2=∥F(x)−(z∗−d1λ)∥d_{2}=\left\|F(x)-\left(z^{*}-d_{1} \lambda\right)\right\|

  其中 θ 是一个预设的惩罚因子，下图给出了该方法的示意图，可知算法放宽了对解的限制，由于惩罚因子的加入，所构成的单目标函数的解可以不仅仅约束在由 λ 所构成的射线上，但偏离的距离 d2 越大，收到的惩罚越厉害。

# 二、MOEA/D 框架（以切比雪夫聚合法为例）

# 2.1 基本定义

  求解 PF 近似解的 MOP 问题可以分解成 N 个单目标优化子问题，这也就意味着需要 N 个不同的权重向量。 MOEA/D 算法在一次运行过程中同时优化 N 个目标函数。对于拥有和 λi 很接近的权重向量对于优化使用 λi 构成的单目标函数会有很大帮助，这是 MOEA/D 算法很重要的机制之一。

# 2.2 “邻居” 定义

   在 MOEA/D 算法中，权重向量 λi 的邻居定义为所有其他 N-1 个权重向量中最接近的一组权重向量。种群由迄今为止每个子问题找到的最优解组成，进利用当前子问题的近邻子问题的解来优化当前子问题。

# 2.3 符号定义

  • NN 个点x1,⋯ ,xN∈Ω\mathrm{x}^{1}, \cdots, \mathrm{x}^{\mathrm{N}} \in \Omega 组成的一个种群，其中xix^i 是第ii 个子问题的当前解；
  • FV1,⋯ ,FVN\mathrm{FV}^{1}, \cdots, \mathrm{FV}^{\mathrm{N}}，其中\mathrf{FV}^{i} 是xix^i 的目标函数值向量
  • z=(z1,⋯ ,zm)T\mathrm{z}=\left(\mathrm{z}_{1}, \cdots, \mathrm{z}_{\mathrm{m}}\right)^{\mathrm{T}}，其中ziz_i 是目标函数fif_i 迄今为止找到的每个目标最优值；
  • 外部种群 EP , 用于存储搜索过程中找到的非支配解。

# 2.4 算法步骤

# 输入输出

  • 输入： MOP ；停止条件（迭代次数）； N （子问题个数）；均匀分布的 N 个权重向量λ1,…,λN\lambda^{1}, \ldots, \lambda^{\mathrm{N}}；每个权重向量的邻居个数 T 。
  • 输出： EP （搜索到的非支配解）。

# 初始化

  • 设定一个空集 EP ；
  • 计算任意两个权重向量之间的欧氏距离，然后求解出每个权重向量的 T 个邻居。B(i)={i1,⋯ ,iT}\mathrm{B}(\mathrm{i})=\left\{\mathrm{i}_{1}, \cdots, \mathrm{i}_{\mathrm{T}}\right\} 表示第 i 个子问题的 T 个邻居；
  • 随机初始化种群x=(x1,⋯ ,xN)\mathrm{x}=\left(\mathrm{x}_{1}, \cdots, \mathrm{x}_{\mathrm{N}}\right)，并计算FVi=F(xi)FV_i=F(x_i)；
  • 初始化z=(z1,⋯ ,zm)T\mathrm{z}=\left(\mathrm{z}_{1}, \cdots, \mathrm{z}_{\mathrm{m}}\right)^{\mathrm{T}}，令zi=min⁡{(fi(x1),…,fi(xN)}\mathrm{z}_{\mathrm{i}}=\min \left\{\left(\mathrm{f}_{\mathrm{i}}\left(\mathrm{x}^{1}\right), \ldots, \mathrm{f}_{\mathrm{i}}\left(\mathrm{x}^{\mathrm{N}}\right)\right\}\right.。（注：由于 z* 难以计算，故可使用特定的方法初始化 z* ，并在循环的过程中更新 z* ）

# 迭代循环

对于i=1,…,Ni=1, \ldots, N

  • 基因重组：从子问题 i 的邻居 B(i) 中随机选取两个索引 k 和 l ，然后对这两个子问题的最优解xkx^k 和xlx^l 使用遗传算子生成新解 y ；
  • 新解的改善：对上一步得到的解 y 使用特定的方法进行改善，生成 y' （以防 y 不满足约束条件）；
  • 更新 z* ：对j=1,2,…,m\mathrm{j}=1,2, \ldots, \mathrm{m}，如果zj<fj(y′)\mathrm{z}_{\mathrm{j}}<\mathrm{f}_{\mathrm{j}}\left(\mathrm{y}^{\prime}\right)，则令zj=fj(y′)\mathrm{z}_{\mathrm{j}}=\mathrm{f}_{\mathrm{j}}\left(\mathrm{y}^{\prime}\right)
  • 更新 EP ：从 EP 中移除 y' 支配的解，如果 EP 中不存在支配 y' 的解，那么就将 y' 加入到 EP 中。

# 停止迭代

  在满足停止条件之后停止迭代，否则继续循环。

# 三、一些讨论

更新于 阅读次数 次