首页 最优化

# 一、强度 Pareto 进化算法（SPEA）

   SPEA(Strength Pareto Evolutionary Algorithm) 将已有技术与新技术想结合以并行的找到多个 Pareto 最优解决方案。它与其他多目标 EA 算法的共同点有：

  • 将目前为止发现的非支配解进行存储；
  • 采用 Pareto 优势的概念对个体分配虚拟适应值；
  • 在不破坏多样性的情况下执行聚类以减少存储的非支配解决方案的数量。
      另一方面， SPEA 算法有如下几个独特之处：
  • 个体的适应度仅有存储在外部非支配集中的解决定，与种群中的个体是否互相支配无关紧要；
  • 外部非支配集上的所有解都参与选择；
  • 为了保持种群的多样性，提出了一种新的生态位方法，这种方法是基于 Pareto 的，不需要任何距离参数
      SPEA 的算法流程如下所示：

# 1.1 算法流程

  • （1）生成和一个初始种群 P 并创建一个空的外部非支配集 P' ；
  • （2）复制 P 中的非支配成员到 P' ；
  • （3）移除 P' 中被其他成员支配的解决方案；
  • （4）如果外部存储 P' 的非支配解超过了给定最大数量 N' ，通过聚类的方式进行修剪；
  • （5）为 P 和 P' 中的每个个体计算适应度值；
  • （6）从 P+P' （并集）中选择个体直到填满交配池， SPEA 使用的带替换的二元竞赛选择；
  • （7）运用问题特定的交叉和变异运算符；
  • （8）如果达到最大迭代次数，则停止，否则执行步骤（2）。

# 1.2 适应度计算

  适应度计算分为两个步骤。首先，对外部非支配集 P' 中的个体进行排序，之后对种群 P 中的个体进行评估。

  • 对于P′P^{\prime}，有fi=si=nN+1f_{i}=s_{i}=\frac{n}{N+1}，其中si∈[0,1)s_{i} \in[0,1)，nn 表示P′P^{\prime} 中每个个体支配PP 中解的数量，加 1 保证取值范围；
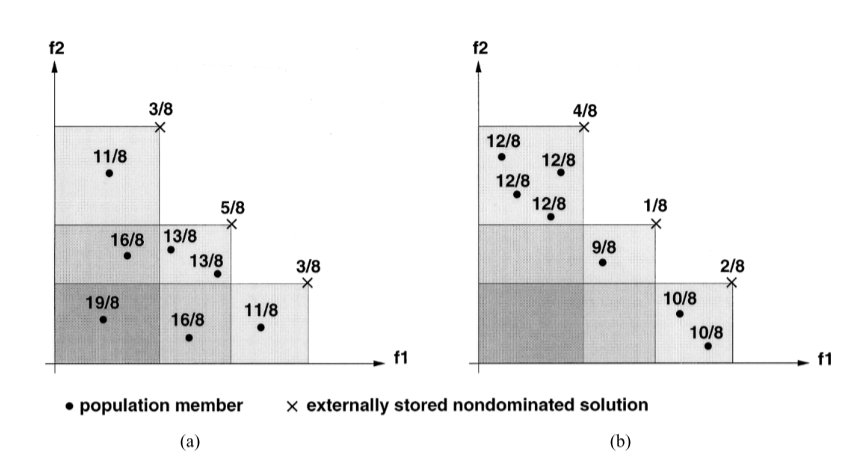
  • 对于PP，有fj=1+∑i,i⪰jsif_{j}=1+\sum_{i, i \succeq j} s_{i}，其中fj∈[1,N)f_j \in [1, N)，∑si\sum s_i 表示将种群PP 中的个体jj 被非支配解集合P′P^{\prime} 中个体ii 的强度值求和。加 1 保证P′P^{\prime} 中的成员比PP 中的成员拥有更好的适应度（注意适应度是最小化的，也就是说，适应度值越小，繁殖概率越高，（自我理解）P′P^{\prime} 中适应度值低的更加分散，从而更加具有多样性）。如下图展示了适应度值的计算：

# 1.3 通过聚类减少 Pareto 集

  非支配解的大小受限制，通过如下步骤进行聚类减少：

  • （1）初始化聚类集CC，每一个外部非支配解i∈P′i \in P^{\prime} 构成一个独立的集群C=⋃i{{i}}C=\bigcup_{i}\{\{i\}\}；
  • （2）如果∣C∣≤N′|C| \leq N^{\prime}，则进行步骤（5），否则进行步骤（3）；
  • （3）计算每个集群对的距离（表示两个集群中个体之间的平均距离），以集群c1c_1 和c2∈Cc_2 \in C 为例，计算公式如下：

d=1∣c1∣⋅∣c2∣⋅∑i1∈c1,i2∈c2∥i1−i2∥d=\frac{1}{\left|c_{1}\right| \cdot\left|c_{2}\right|} \cdot \sum_{i_{1} \in c_{1}, i_{2} \in c_{2}}\left\|i_{1}-i_{2}\right\|

  • （4）通过如下公式将拥有最小距离的两个集群c1c_1 和c2c_2 合并，并返回步骤（2）；

C=C\{c1,c2}∪{c1∪c2}C=C \backslash\left\{c_{1}, c_{2}\right\} \cup\left\{c_{1} \cup c_{2}\right\}

  • （5）确定每个聚类的代表个体。通常选择和同一聚类的其他个体之间的平均距离最小的个体作为该聚类的代表。

# 二、改进强度 Pareto 进化算法（SPEA2）

   SPEA 算法具有如下缺点：

  • Fitness assignment ：被相同外部非支配个体支配的其他个体具有相同的适应度值，这降低了选择压力，使得 SPEA 算法编程了一个随机搜索算法；
  • Density estimation ：如果很多个个体是不相关的，例如不互相支配，则无法从支配关系中获得有效信息；
  • Archive truncation：虽然聚类技术可以在保证算法特征的同时减少非支配解，但是丢失了外部非支配解。

# 2.1 算法步骤

  • （1）初始化：生成一个初始种群P0P_0 并创建一个空的外部集P‾0=∅\overline{\boldsymbol{P}}_{0}=\emptyset；
  • （2）适应度值计算：计算适应度值PtP_t 和P‾t\overline{P}_t，如 2.2 所示；
  • （3）环境选择：复制所有PtP_t 和P‾t\overline{P}_t 中的非支配解到P‾t+1\overline{P}_{t+1}，如果P‾t+1\overline{P}_{t+1} 的大小不等于N‾\overline{N}，则进行其他操作，如 2.3 所示；
  • （4）终止：如果达到了终止条件，那么输出上一步的P‾t+1\overline{P}_{t+1}；
  • （5）交配选择：对P‾t+1\overline{P}_{t+1} 执行二进制锦标赛选择直至填满交配池；
  • （6）变换：对交配池应用基因重组和突变算子，转到步骤（2）。

# 2.2 适应度值计算

  为了避免被同样的外部集成员支配的个体具有相同的适应度值，在 SPEA2 中，每个个体所支配的解和支配它的解都被考虑在内。种群和外部集中的个体ii 都被赋予一个强度值S(i)S(i)，表示受该个体支配的解的数量。

S(i)=∣{j∣j∈Pt+P‾t∧i≻j}∣S(\boldsymbol{i})=\left|\left\{\boldsymbol{j} \mid \boldsymbol{j} \in \boldsymbol{P}_{t}+\overline{\boldsymbol{P}}_{t} \wedge \boldsymbol{i} \succ \boldsymbol{j}\right\}\right|

  在S(i)S(i) 的基础上，个体ii 的原始适应度值R(i)R(i) 等于支配该个体的所有个体的强度值之和，即：

R(i)=∑j∈Pt+P‾t,j≻iS(j)R(\boldsymbol{i})=\sum_{\boldsymbol{j} \in \boldsymbol{P}_{t}+\overline{\boldsymbol{P}}_{t}, \boldsymbol{j} \succ \boldsymbol{i}} S(\boldsymbol{j})

  与 SPEA 不同，计算R(i)R(i) 时，种群和外部档案内的个体都考虑在内，而且原始适应度值越小，说明支配该个体的个体少，R(i)=0R(i)=0 表示个体ii 为非支配解。 SPEA （左）和 SPEA2 （右）的在适应度计算方法的示意图如下图所示：

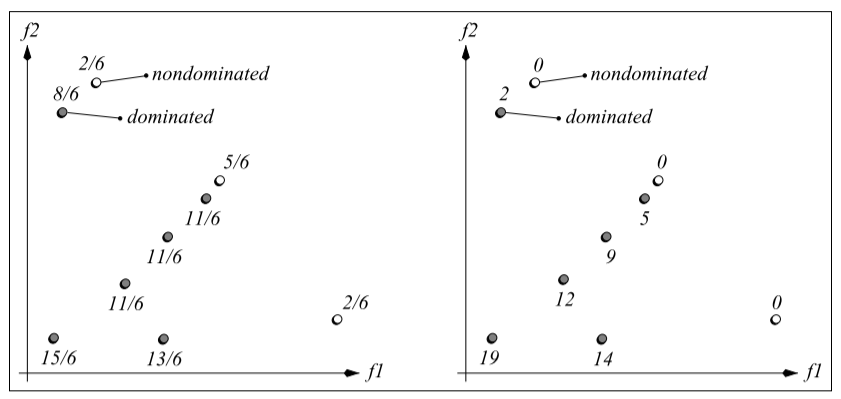
  原始适应度赋值过程引入密度信息以区分具有相同原始适应度值的个体。 SPEA2 采用kk 紧邻方法来计算个体ii 的密度值D(i)D(i)：

D(i)=1σik+2D(\boldsymbol{i})=\frac{1}{\sigma_{i}^{k}+2}

  以上式子中，σik\sigma_{i}^{k} 为个体ii 与第kk 个近邻个体在目标空间上的距离，在该算法中，k 的取值为种群和外部集大小和的平方根，即：

k=N+N‾k=\sqrt{N+\overline{N}}

  最终，个体ii 的适应度值F(i)F(i) 为原始适应度值与密度值之和：

F(i)=R(i)+D(i)F(\boldsymbol{i})=R(\boldsymbol{i})+D(\boldsymbol{i})

# 2.3 环境选择

  与 SPEA 中更新操作有如下两个不同：（1）外部集中包含个体的数量随时间变化不变；（2）使用截断方法防止边界解被删除。
  首先将复制所有PtP_t 和P‾t\overline{P}_t 中的非支配解到P‾t+1\overline{P}_{t+1}；
  设定外部非支配解P‾t+1\overline{P}_{t+1} 的数量等于N‾\overline{N}，有如下三种情况：

  • 选出的P‾t+1\overline{P}_{t+1} 数量刚好等于N‾\overline{N}；
  • 选出的P‾t+1\overline{P}_{t+1} 数量少于N‾\overline{N}，则需要按照适应度值排序，补选 “非支配解” 进入P‾t+1\overline{P}_{t+1}；
  • 选出的P‾t+1\overline{P}_{t+1} 数量多于N‾\overline{N}，则需要进行截断操作， SEPA2 使用迭代法，利用kk 紧邻法每一次去除和周围第kk 个临近点距离最近的点，直到数量减少到设定值N‾\overline{N}。
更新于 阅读次数 次