参考链接：https://blog.csdn.net/weixin_51772802/article/details/128767706、https://blog.csdn.net/tauyangdao/article/details/108058222

# 一、什么是 LQR

  在讨论 LQR 基本原理时，被控对象一般都是线性定常系统，即系统状态不随时间变化的系统，状态空间表达式如下：

$$\begin{array}{l} \dot{x}=A x+B u \\ y=C x+D u \end{array}$$

   LQR 控制通过设定一个线性反馈控制器$u=-Kx$，用以得到输入参数$u$ 和状态变量$x$ 的关系，全状态反馈控制器的状态空间描述框图如下图所示：

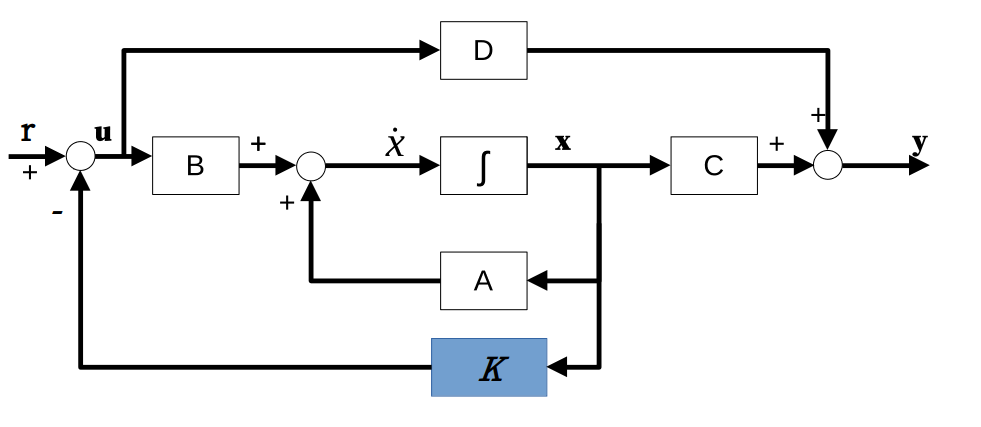
  从而第一行可以写为

$$\dot{x}=A x-B K x=\underbrace{(A-B K)}_{A_{c l}} x$$

  让系统稳定的条件是矩阵$A_{cl}$ 的特征值的实部均为负数，我们可以手动选择几个满足上述条件的特征值，然后反解$K$，从而得到控制器。而 LQR 的出现，就是为了让几个参数的选择更为合理，从而使得控制器控制效果更好。
  其实现方式正是通过设计代价函数$J$ 实现的。无限时间的 LQR 问题设计的成本代价泛函$J$ 为：

$$J=\int_{0}^{\infty}\left(x^{T} Q x+u^{T} R u\right) d t, Q=Q^{T}, R=R^{T}, Q \geq 0, R>0$$

  一般来说，$Q$ 阵和$R$ 阵为对角阵，分别确定了状态变量$x$ 和输入参数$u$ 的权重。对角阵上的值越大说明我们设计时对于该量的重视程度越大，即希望这个量在变化过程中保持较小的值，换种说法就是对于该量的 “惩罚” 越大。我们的设计目标就是得到一系列的控制序列使代价累积的最小。上式的推导过程可见下图：

  因此，问题就转变为了选择合适的反馈矩阵$K$ 使得代价函数$J$ 最小。
  在 matlab 中可以直接使用相关命令矩阵得到$K$ 阵

K=lqr（A，B，Q，R）

# 二、LQR 控制器的设计步骤

• （1）根据期望状态，初步设计好$Q$ 阵和$R$ 阵；
• （2）根据代数 Riccati 方程求解 P 矩阵（大多数情况使用数值解法，很少情况可以求解析解）
• （3）根据$P$，得到反馈矩阵$K$ 的表达式，从而得到最优控制序列。
    其中，代数 Riccati 方程表达式如下：

$$P A+A^{T} P-P B R^{-1} B^{T} P+Q=0$$

  反馈矩阵$K$ 的表达式如下：

$$K=R^{-1} B^{T} P$$

# 三、Riccati 方程推导过程

# 四、稳定性分析

  稳定性分析证明如下所示，需要注意的是，公式 (8) 即为 Riccati 方程。