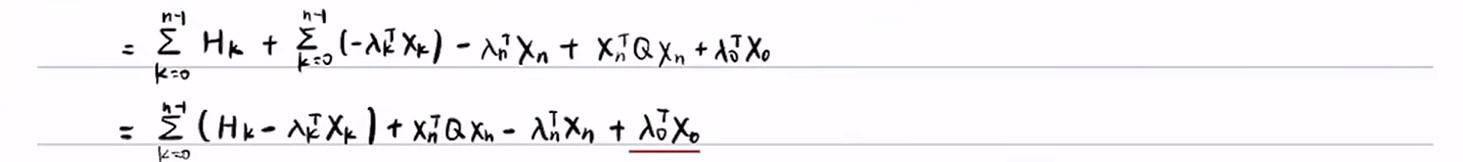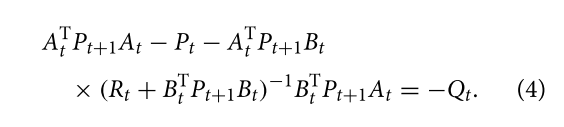参考链接：https://www.bilibili.com/video/BV1P54y1m7CZ/?spm_id_from=333.337.search-card.all.click&vd_source=e01172ea292c1c605b346101d7006c61

# 一、什么是离散 LQR

  连续 LQR 问题可以参考上一篇文章，离散 LQR 问题即将连续 LQR 进行离散化处理，离散状态空间表达式如下：

$$x_{k+1}=A_k x_k+B_k u_k$$

  代价函数$J$ 的离散化表达式如下：

$$J=\sum_{k=0}^{\infty}\left(x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}\right) , Q=Q^{T}, R=R^{T}, Q \geq 0, R>0$$

  为了方便计算，将$J$ 使用如下形式进行表达（由于离散状态空间表达式中包含$x_{k}$、$x_{k+1}$ 以及$u_k$，故$x$ 的下标要多一位，$n$ 趋于无穷）：

$$J=\sum_{k=0}^{n-1}\left(x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}\right) + x_{n}^{T} Q x_{n}, Q=Q^{T}, R=R^{T}, Q \geq 0, R>0$$

# 二、离散 LQR 公式推导

  在离散 LQR 公式的推导中，需要使用拉格朗日乘子法，以第三个式子为目标函数，第一个式子为约束条件，从而构造拉格朗日函数如下：

$$J=\sum_{k=0}^{n-1}\left(x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}\right) + x_{n}^{T} Q x_{n}+\sum_{k=0}^{n-1}\lambda_{k+1}\left( A x_k+B u_k -x_{k+1}\right)$$

  将上式进行如下化简：

  对上述过程的最终结果对变量$x_{k}$ 和$u_k$ 以及$\lambda$ 进行求导可得如下结果：

  根据$H_k$ 的定义进行求导有：

  带入求导结果中可得：

  我们最要得到的是$u_k$，根据式$2$ 可知$u_k$ 可由$\lambda_{k+1}$ 唯一求得，而根据式$1$ 可知$\lambda_{k+1}$ 与$\lambda_k$ 相关，而式$4$ 可以求出$\lambda_n$，故可以使用递推的方式进行求解，下图展示了由$\lambda_n$ 递推得到$\lambda_{n-1}$ 的演算过程：

  由上式推导过程推广到一般式可得递归关系，也就是 Riccati 方程如下所示：

  一般使用的 Riccati 方程形式如下，可由上式推导得出：

# 三、离散 LQR 的 matlab 求解

  在 matlab 中可以使用 [K,S,e] = dlqr(A,B,Q,R) 进行求解，其中$K$ 为全状态反馈矩阵，其他两个参数含义可在 matlab 文档中获取，$K$ 的定义可参考连续 LQR 文章，$K$ 的计算公式如下：

$$K_k=\left(R+B^{\mathrm{T}} P_{k+1} B\right)^{-1} B^{\mathrm{T}} P_{k+1} A_{k}$$

$$u_k=-\left(R+B^{\mathrm{T}} P_{k+1} B\right)^{-1} B^{\mathrm{T}} P_{k+1} A_{k} x_{k}$$

# 四、离散 LQR 总结

• （1）将连续系统离散化，得到离散系统；
• （2）求解 Riccati 方程，获得$P_k$ 的序列；
• （3）使用第三节中的公式求解反馈矩阵$K_k$ 的序列；
• （4）使用第三节中的公式求解反馈矩阵$u_k$ 的序列；