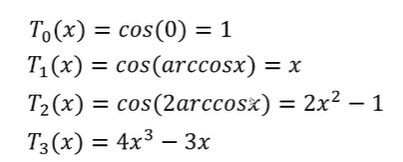参考:https://www.bilibili.com/video/BV1eT4y1K7DL/?spm_id_from=333.999.0.0
# 一、问题的提出
函数逼近:
逼近与拟合的区别:
- 逼近指的是用连续函数 “逼近” 连续函数
- 拟合指的是用连续函数 “拟合” 离散数据
逼近(拟合)和插值的区别
- 逼近(拟合)并不要求获得的函数通过已知点,只要尽量接近
- 插值要求获得的函数必须经过已知点
函数逼近的第一个问题:如何表示 “尽量接近”?
- 一致逼近:最大的偏差也不超过 xxx
- 平方逼近:平方偏差和不超过 xxx
# 二、相关概念
# 2.1 离散数据的最佳平方逼近
设已知一段测得的数据
(xi,yi),(i=1,2,⋯,m>>n)
构造一个近似函数s(x) 去逼近所求函数y=f(x)
那么离散数据的最佳平方逼近为:
∥δ∥22=i=0∑mδi2=i=0∑m[s∗(xi)−f(xi)]2
# 2.2 线性无关函数族
线性无关函数族的表达式如下:
S=span{x1,...,xn}
其中x1,...,xn 线性无关。最典型的线性无关函数族即1,x,x2,...,xn
所谓函数族,就是做逼近或拟合的 “素材库”,可以从 “库” 中选择一个或多个函数组合成逼近用的新函数。
# 2.3 权函数
有些点比较重要,应该更接近,而有些点不那么重要。相当于给每一个点乘以一个权重值ω。因为每一个点对应一个权重值,那么这个权重ω 可以看作一个函数,称为权函数ω(x)。
加入权重后,离散数据的最佳平方逼近可以更一般的表示为:
∥δ∥22=i=0∑mδi2=i=0∑mω(xi)[s∗(xi)−f(xi)]2=s(x)∈Φmini=0∑mω(xi)[s(xi)−f(xi)]2
问题归结为求s∗(x)=∑k=0nakφk(x),即求系数ak,使得下式取得最小值
I(a0,⋯,an)=i=0∑mω(xi)[k=0∑nakφk(xi)−f(xi)]2
对ak 求偏导数,可以得到
21∂aj∂I=i=0∑mω(xi)φj(xi)[f(xi)−k=0∑nakφk(xi)],j=0,1,2,..., n
令偏导为 0,得到
i=0∑mω(xi)φj(xi)[f(xi)−k=0∑nakφk(xi)]=0
展开可以得到
k=0∑naki=0∑mω(xi)φj(xi)φk(xi)=i=0∑mω(xi)φj(xi)f(xi)
# 2.4 内积
∑i=0mω(xi)fj(xi)gk(xi) 可以写作(f,g),表示带权的内积。
从而 2.3 的最后一个式子可以表达为:
k=0∑nak(φj,φk)=(φj,f)
# 2.5 正规方程组
将 2.4 的最后一个式子展开为:
a0(φj,φ0)+a1(φj,φ1)+⋯an(φj,φn)+=(φj,f)
由于上式只对应了其中一个j,一共有n+1 个类似的方程,因此可以得到:
⎣⎢⎢⎢⎢⎡(φ0,φ0)(φ1,φ0)⋮(φn,φ0)(φ0,φ1)(φ1,φ1)⋮(φn,φ1)⋯⋯⋯⋯(φ0,φn)(φ1,φn)⋮(φn,φn)⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡a0a1⋮an⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡(φ0,f)(φ1,f)⋮(φn,f)⎦⎥⎥⎥⎥⎤
上述方程组被称为正规方程组(法方程组),左边的矩阵被称为 Cramer 矩阵。
# 2.6 正交函数族
当直接使用 2.2 中的一般无关线性族时,会产生病态矩阵,从而导致求解误差大的问题。因此引入正交函数族。
正交函数族就是所有函数在函数空间上都 “两两垂直”,即两个函数求内积为 0。因此 2.5 中的最后一个式子可以表达为:
⎣⎢⎢⎢⎢⎡(φ0,φ0)0⋮00(φ1,φ1)⋮0⋯⋯⋯⋯00⋮(φn,φn)⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡a0a1⋮an⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡(φ0,f)(φ1,f)⋮(φn,f)⎦⎥⎥⎥⎥⎤
正规方程组的 Cramer 矩阵直接变成了对角阵,求解变的更加简单。并且避免了病态矩阵的问题。
# 三、正交多项式
# 3.1 定义
若首项系数an=0 的n 次多项式gn(x) 满足
∫abρ(x)gi(x)gk(x)dx={0,i=k,Ak>0,i=k,(i,k=0,1,2,⋯)
则称函数族g0(x),g1(x),... 在[a,b] 上带权正交。
# 3.2 性质
- 性质 1:线性无关
- 性质 2:零点都是实的,相异的,全部在(a,b) 内部
- 性质 3:任意相邻 3 个多项式存在如下关系:
pn+1(x)=(x−αn)pn(x)−βnpn−1(x),n=0,1,⋯,
其中
p0(x)=1
p−1(x)=0
αn=(pn,pn)(xpn,pn)
βn=(pn−1,pn−1)(pn,pn)
因此,只需要知道前两个多项式,其他的多项式就可以递推出来。注意,如果权函数发生变化,多项式就会不同。
# 3.3 常见多项式
# (1)勒让德多项式
勒让德多项式的前几项为:
![]()
勒让德多项式的区间为 [-1, 1],权函数ρ≡1,n 次勒让德多项式的表达式为:
Pn(x)=2nn!1dxndn[(x2−1)n],(n=0,1,2,⋯⋯)
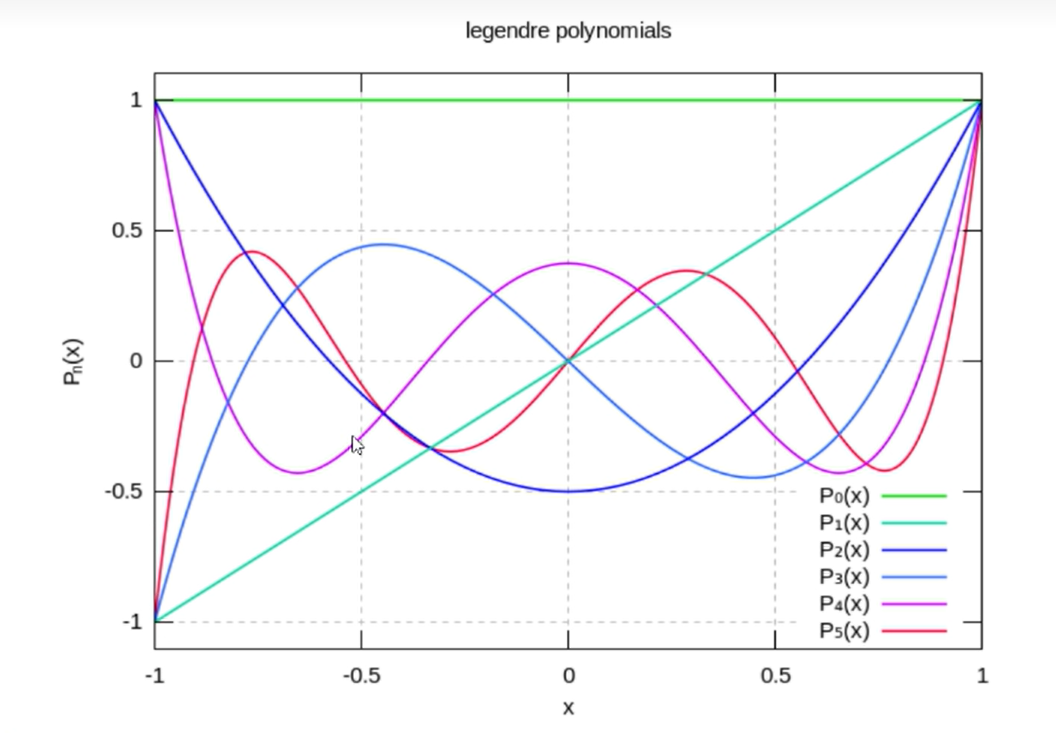
勒让德多项式的图像为:
![]()
勒让德多项式的三个性质如下
∫−11Pm(x)Pn(x)dx={0,2n+12m=n,m=n.
- 奇偶性,当n 是偶数时是偶函数,奇数时是奇函数
Pn(−x)=(−1)nPn(x)
P0(x)=1,P1(x)=x,Pn+1(x)=n+12n+1xPn(x)−n+1nPn−1(x)
# (2)切比雪夫多项式(Type Ⅰ)
切比雪夫多项式的前几项为:
![]()
切比雪夫多项式的区间为 [-1, 1],权函数ρ=1−x21,n 次切比雪夫多项式的表达式为:
Tn(x)=cos(narccos(x)),(n=0,1,2,⋯⋯)
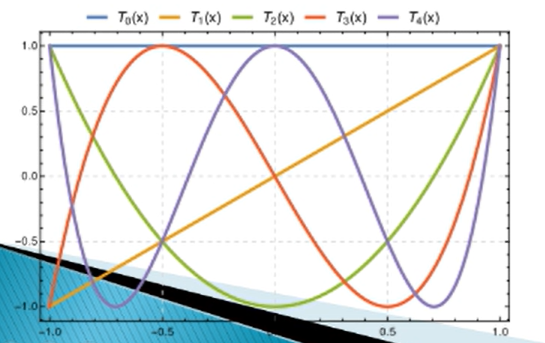
切比雪夫多项式的图像为:
![]()
切比雪夫多项式的三个性质如下
∫−111−x21Tm(x)Tn(x)dx=0,m=n{π/2,m=n=0π,m=n=0
- 奇偶性,当n 是偶数时是偶函数,奇数时是奇函数
Tn(−x)=(−1)nTn(x)
{T0(x)=1,T1(x)=x,Tn+1(x)=2xTn(x)−Tn−1(x).
# (3)其他正交多项式
- 切比雪夫多项式(Type Ⅱ)
- 拉盖尔多项式
- 埃尔米特多项式
# 四、正交多项式做最佳平方逼近
当基函数用正交函数族时,法方程组会变成:
⎣⎢⎢⎢⎢⎡(φ0,φ0)0⋮00(φ1,φ1)⋮0⋯⋯⋯⋯00⋮(φn,φn)⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡a0a1⋮an⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡(φ0,f)(φ1,f)⋮(φn,f)⎦⎥⎥⎥⎥⎤
从而
ak∗=(f,φk)/(φk,φk)
因此,最佳逼近多项式为:
sn∗(x)=k=0∑nak∗φk(x)=k=0∑n∣∣φk∣∣22(f,φk)φk(x)
如果使用勒让德多项式,那么
ak∗=(f,φk)/(φk,φk)=22k+1(f,φk)
即可求出所需要的系数。如果目标函数的函数范围不在 [-1,1],那么可以使用缩放的方式,投影到 [-1,1] 上进行运算。
# 五、正交多项式做最小二乘拟合
对于最小二乘拟合问题,一般不适用现成的正交式,而是现推正交多项式,因为:
- 最小二乘拟合问题相对简单(主要体现在内积容易求)
- 如果用以后的正交多项式,变量的替换也很麻烦
- 这种处理方式会变成循环递推,易于编程
具体的处理方法为:
pn+1(x)=(x−an)pn(x)−bnpn−1(x),n=0,1,⋯,
其中
p0(x)=1
p−1(x)=0
αn=(pn,pn)(xpn,pn)
βn=(pn−1,pn−1)(pn,pn)
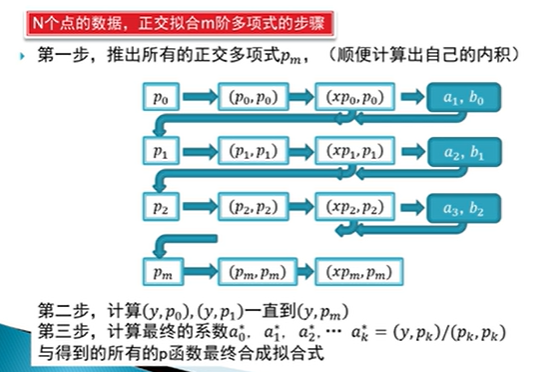
具体流程:
![]()