参考文章：https://blog.csdn.net/MoreAction_/article/details/106443383

# 一、要解决的问题

  在工程引用中，我们经常会用一组观测数据去估计模型的参数，模型是我们根据先验知识定下的。比如我们有一组观测数据 $(x_i, y_i), i=1...n$，通过一些数据分析我们猜测$y$ 和$x$ 之间存在线性关系，那么我们的模型就可以定为：

$$f(x)=kx+b$$

  这个模型只有两个参数，所以理论上，我们只需要观测两组数据建立两个方程，即可解出两个未知数。类似的，假如模型有$n$ 个参数，我们只需要观测$n$ 组数据就可求出参数，换句话说，在这种情况下，模型的参数是唯一确定解。

  但是在实际应用中，由于我们的观测会存在误差（偶然误差、系统误差等），所以我们总会做多余观测。比如在上述例子中，尽管只有两个参数，但是我们可能会观测$n$ 组数据$(x_1, y_1), ..., (x_n, y_n)$，这会导致我们无法找到一条直线经过所有的点，也就是说，方程无确定解。如下图所示：

  于是这就是我们要解决的问题：虽然没有确定解，但是我们能不能求出近似解，使得模型能在各个观测点上达到 “最佳 “拟合。早在 19 世纪，勒让德就认为让 “误差的平方和最小” 估计出来的模型是最接近真实情形的。按照勒让德的最佳原则，于是就是求：

$$L=\sum_{i=1}^{n}\left ( y_i-f\left ( x \right ) \right ) ^2$$

  这个目标函数取得最小值时的函数参数，这就是最小二乘法的思想，所谓 “二乘” 就是平方的意思。从这里我们可以看到，最小二乘法其实就是用来做函数拟合的一种思想。

# 二、最小二乘法

  线性回归定义为：$h_{\theta }(x_1,x_2,...,x_{n-1})=\theta_0+\theta_1x_1+...+\theta_{n-1}x_{n-1}$，其中$\theta$ 是要求解的参数。假设现在有$m$ 个样本，每一个样本都有$n-1$ 维度的特征，将所有样本点带入模型中可得：

$$\begin{aligned} & \mathrm{h}_1=\theta_0+\theta_1 \mathrm{x}_{1,1}+\theta_2 \mathrm{x}_{1,2}+\ldots+\theta_{\mathrm{n}-1} \mathrm{x}_{1, \mathrm{n}-1} \\ & \mathrm{~h}_2=\theta_0+\theta_1 \mathrm{x}_{2,1}+\theta_2 \mathrm{x}_{2,2}+\ldots+\theta_{\mathrm{n}-1} \mathrm{x}_{2, \mathrm{n}-1} \\ & \vdots \\ & \mathrm{h}_{\mathrm{m}}=\theta_0+\theta_1 \mathrm{x}_{\mathrm{m}, 1}+\theta_2 \mathrm{x}_{\mathrm{m}, 2}+\ldots+\theta_{\mathrm{n}-1} \mathrm{x}_{\mathrm{m}, \mathrm{n}-1} \end{aligned}$$

  为方便用矩阵表示，我们令$x_0 = I$，于是上述方程可以用矩阵表示为：

$$\mathbf{h}=\mathbf{X}\mathbf{\theta}$$

  其中，$\mathbf{h}$ 为$m\times 1$ 的向量，代表模型的估计值，$\thetaθ$ 为$n\times 1$ 的向量，$\mathbf{X}$ 为$m\times n$ 维的矩阵，$m$ 代表样本的个数，$n$ 代表样本的特征数，于是目标损失函数用矩阵表示为：

$$J(\theta)=\left \| \mathbf{h}-\mathbf{Y} \right \| ^2=\left \| \mathbf{X}\theta-\mathbf{Y} \right \| ^2=(\mathbf{X}\theta-\mathbf{Y})^{\mathrm{T}}(\mathbf{X}\theta-\mathbf{Y})$$

  其中$\mathbf{Y}$ 是样本的标准输出向量，维度为$m\times 1$。对目标函数进行求导，并令其导数等于 0，可以得到：

$$\frac{\partial }{\partial \theta} J(\theta)=2\mathbf{X}^{\mathrm{T}}\mathbf{X}\theta-2\mathbf{X}^{\mathrm{T}}\mathbf{Y}=0$$

  解得：

$$\theta=(\mathbf{X}^{\mathrm{T}}\mathbf{X})^{-1}\mathbf{X}^{\mathrm{T}}\mathbf{Y}$$

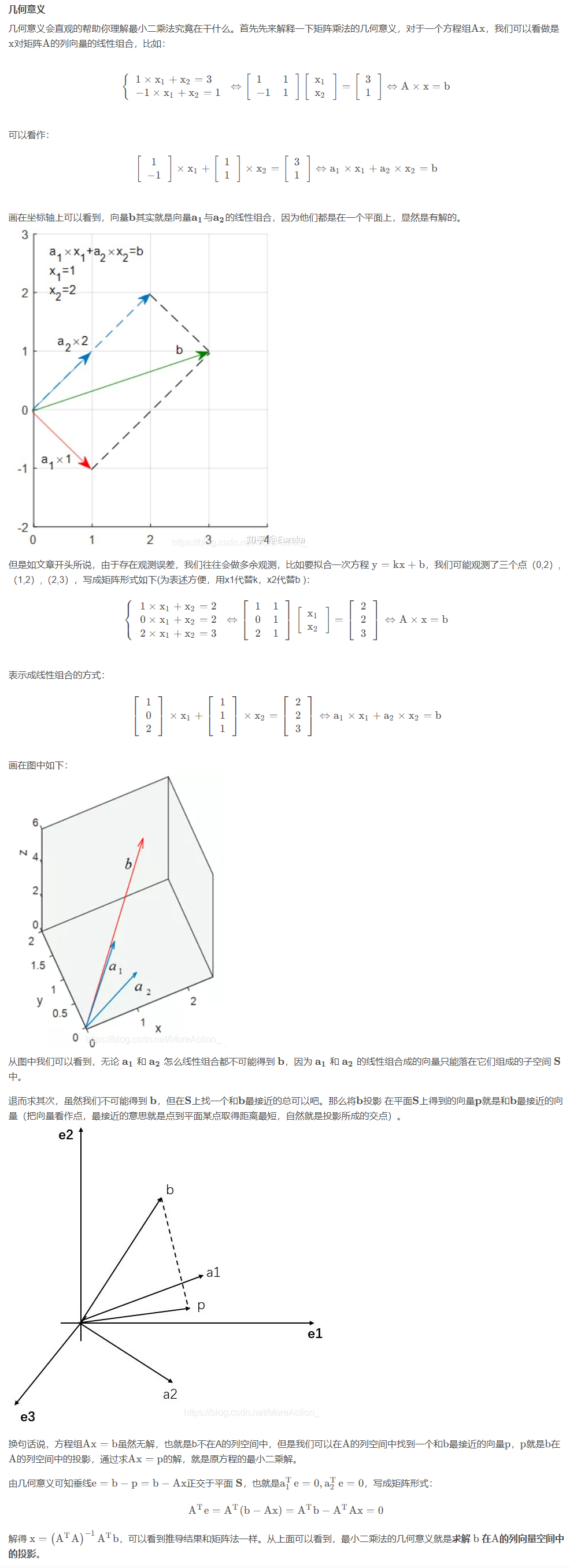
# 三、几何意义

# 四、岭回归

  核心求解公式：

$$\theta=(\mathbf{X}^{\mathrm{T}}\mathbf{X}+\lambda\mathrm{I})^{-1}\mathbf{X}^{\mathrm{T}}\mathbf{Y}$$