首页 AI

参考链接：https://blog.csdn.net/DFCED/article/details/132394895、https://www.bilibili.com/video/BV1QAexeiEZK?p=2&vd_source=e01172ea292c1c605b346101d7006c61

  扩散概率模型（为简洁起见，我们称之为 “扩散模型”）是一种通过参数化的马尔科夫链，并使用变分推断进行训练，以在有限时间后生成与数据相匹配的样本。该链的转换过程旨在学习逆向扩散过程，即一个马尔科夫链，该链逐步向数据中添加噪声，方向与采样相反，直到信号完全被破坏。

# 一、直观理解

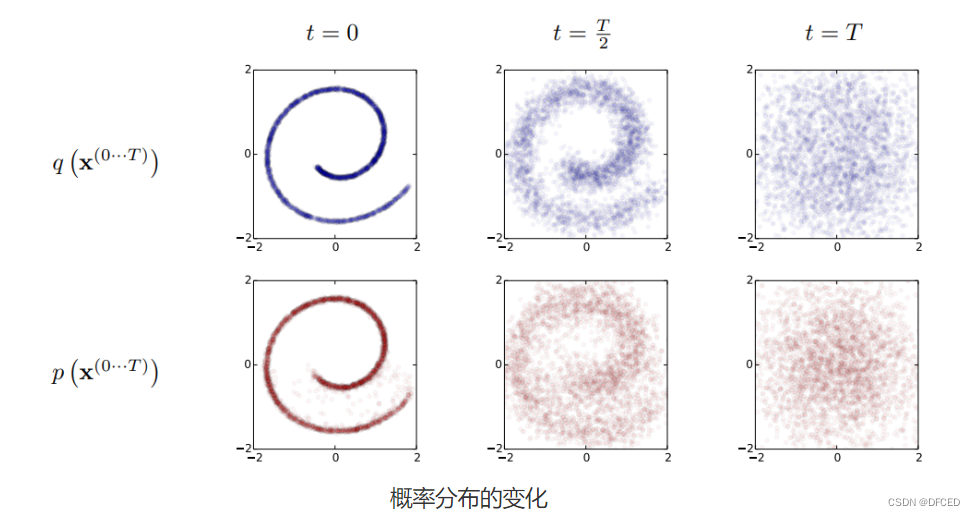
  从概率分布角度来看，考虑下图瑞士卷形状的二维联合概率分布 P (x,y)，扩散过程 q 非常直观，本来集中有序的样本点，受到噪声的扰动，向外扩散，最终变成一个完全无序的噪声分布。

  而 diffusion model 表示上图的逆过程 p，将一个噪声分布 N (0,1) 逐步的去噪以映射到原始图像。有了这样的映射，就可以从噪声分布中采样，最终得到一张想要的图像，也就是完成了生成的任务。

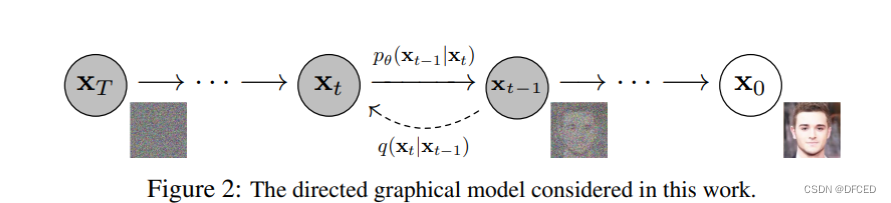
  Diffusion Models 由正向过程（或扩散过程）和反向过程（或逆扩散过程）组成，其中输入数据逐渐被噪声化，然后噪声被转换回源目标分布的样本。从单个图像样本来看这个过程，扩散过程 q 就是不断向图像上加噪声，直到图像变成一个纯噪声，逆扩散过程 p 就是从纯噪声生成一张图像的过程。下图表示了单个样本图像的变化：

  一些相关的概念：

  • 后验概率：在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率（Posterior probability）是在考虑和给出相关证据或数据后所得到的条件概率。
  • 马尔可夫链：为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备 “无记忆” 的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的 “无记忆性 “称作马可夫性质。

# 二、前向过程（扩散过程）

  所谓前向过程，即往图片上加噪声的过程。虽然这个步骤无法做到图片生成，但是这是理解 diffusion model 以及构建训练样本至关重要的一步。

  给定真实图片样本 x0∼q(x)x_{0}\sim q(x)，diffusion 前向过程通过TT 次累计对其添加高斯噪声，得到x1,x2，…,xTx_1, x_2，\dots, x_T，如下图的 q 过程。每一步的大小是由一系列的高斯分布方差的超参数{βt∈(0,1)}t=1T\{\beta_t\in(0,1)\}_{t=1}^T 来控制的。前向过程由于每个时刻tt 只与t−1t-1 时刻有关，所以也可以看做马尔科夫过程：

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t\mathbf{I})

q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(x_{1:T}|x_0)=\prod_{t=1}^Tq(x_t|x_{t-1})

  这个过程中，随着tt 的增大，xtx_t 越来越接近纯噪声。当T⇒∞T\Rightarrow \infty，xTx_T 是完全的高斯噪声。

  前向过程介绍结束前，需要讲述一下 diffusion 在实现和推导过程中要用到的两个重要特性。

  • 特性 1：重参数 （reparameterization trick）

  重参数技巧在很多工作（gumbel softmax, VAE）中有所引用。如果我们要从某个分布中随机采样（高斯分布）一个样本，这个过程是无法反传梯度的。而这个通过高斯噪声采样得到xtx_t 的过程在 diffusion 中到处都是，因此我们需要通过重参数技巧来使得他可微。最通常的做法是把随机性通过一个独立的随机变量（$\epsilon ）引导过去。即如果要从高斯分布）引导过去。即如果要从高斯分布 z\sim\mathcalN}(z;\mu_\theta,\sigma_\theta【2\mathbf{I】)采样一个采样一个 z$，我们可以写成：

z=μθ+σθ⊙ϵ,ϵ∼N(0,I)z=\mu_\theta+\sigma_\theta\odot\epsilon,\epsilon\sim\mathcal{N}(0,\mathbf{I})

  上式的zz 依旧是有随机性的，且满足均值为μθ\mu_\theta 方差为σθ\sigma_\theta 的高斯分布。这里的μθ\mu_\theta，σθ\sigma_\theta 可以是由神经网络推断得到的。整个 “采样” 过程依旧梯度可导，随机性被转嫁到了 $\epsilon $ 上。

  • 特征 2：任意时刻的xtx_t 可由x0x_0 和βt\beta_t 表示

  在前向过程中，有一个性质非常棒，就是我们其实可以通过x0x_0 和βt\beta_t 直接得到xtx_t。首先我们令αt=1−βt\alpha_t=1-\beta_t，并且α‾t=∏i=1tαi\overline{\alpha}_t=\prod_{i=1}^t\alpha_i，展开xtx_t 可以得到：

xt=αtxt−1+1−αtϵt−1=αtαt−1xt−2+1−αtαt−1ϵˉt−2=…=αˉtx0+1−αˉtϵ\begin{aligned} \mathbf{x}_{t}& =\sqrt{\alpha_t}\mathbf{x}_{t-1}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{t-1} \\ &=\sqrt{\alpha_t\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\bar{\boldsymbol{\epsilon}}_{t-2} \\ &=\ldots \\ &=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon} \end{aligned}

  因此，任意时刻的xtx_t 满足：

q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)q(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t)\mathbf{I})

# 三、反向过程（逆扩散过程）

  如果说前向过程（forward）是加噪的过程，那么逆向过程（reverse） 就是 diffusion 的去噪推断过程。

  如果我们能够逆转上述过程并从q(xt−1∣xt)q(x_{t-1}\mid x_t) 采样，就可以从高斯噪声xT∼N(0,I)x_{T}\sim\mathcal{N}(0,\mathbf{I}) 还原出原图分布x0∼q(x)x_0 \sim q(x)。在文献 7 中证明了如果q(xt∣xt−1)q(x_{t}\mid x_{t-1}) 满足高斯分布且βt\beta_t 足够小，q(xt−1∣xt)q(x_{t-1}\mid x_t) 仍然是一个高斯分布。然而我们无法简单推断q(xt−1∣xt)q(x_{t-1}\mid x_t)，因此我们使用深度学习模型（参数力θ\theta，目前主流是 U-Net + attention 的结构）去预测这样的一个逆向的分布pθp_{\theta}（类似 VAE）：

pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt);p_\theta(x_{0:T})=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t);

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)).p_\theta(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)).

  由此可以发现其实正向扩散和逆扩散过程都是马尔可夫，然后正态分布，然后一步一步条件概率的框架。唯一的区别就是正向扩散里每一个条件概率的高斯分布的均值和方差都是
已经确定的（依赖于βt\beta_t 和x0x_0），而逆扩散过程里面的均值和方差是我们网络要学出来。

# 逆扩散条件概率推导

  虽然我们无法得到逆转过程的概率分布q(xt−1∣xt)q(x_{t-1}\mid x_t)，但是如果知道x0x_0，q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0) 就可以直接写出，大概形式如下：

q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}(x_t,x_0),\tilde{\beta}_t\mathbf{I})

  通过一定的计算可以得到上式中的均值和方差为：

β~t=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_t

μ~t=1αt(xt−1−αt1−α‾tϵt)\tilde{\mu}_t=\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_t)

  可以看出，在给定x0x_0 的条件下，后验条件高斯分布的均值只和超参数，xtx_t，ϵ\epsilon 有关，方差只与超参数有关。

# 四、训练损失

  了解了上述逆扩散过程之后，如何训练 Diffusion Models 以求得后验条件高斯分布的均值μθ(xt,t)\mu_{\theta}(x_t,t) 和方差Σθ(xt,t)\Sigma_{\theta}(x_t,t) 呢？

  对于真实的训练样本数据已知，要求模型的参数，可以使用极大似然估计。Diffusion Models 通过极大似然估计，来找到逆扩散过程中马尔可夫链转换的概率分布，这就是 Diffusion Models 的训练目的。即最大化模型预测分布的对数似然，从 Loss 下降的角度就是最小化负对数似然：

L=Eq[−log⁡pθ(x0)]\mathcal{L}=\mathbb{E}_q[-\log p_\theta(x_0)]

  通过一定的推导可以得到如下损失函数：

Lt=Ex0,ϵ[∥1αt(xt−βt1−αˉtϵ)−1αt(xt−βt1−αˉtϵθ(xt,t))∥2]ϵ∼N(0,1)=Ex0,ϵ[∥ϵ−ϵθ(xt,t)∥2]ϵ∼N(0,1)=Ex0,ϵ[∥ϵ−ϵθ(α‾tx0+1−α‾tϵ,t)∥2],ϵ∼N(0,1)\begin{aligned} L_{t}& =\mathbb{E}_{\mathbf{x}_{0},\epsilon}\left[\left\|\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon\right)-\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(\mathbf{x}_{t},t)\right)\right\|^{2}\right]\quad\epsilon\sim\mathcal{N}(0,1) \\ &=\mathbb{E}_{\mathbf{x}_0,\epsilon}\left[\left\|\epsilon-\epsilon_\theta(\mathbf{x}_t,t)\right\|^2\right]\quad\epsilon\sim\mathcal{N}(0,1) \\ &=\mathbb{E}_{\mathbf{x}_0,\epsilon}\left[\left\|\epsilon-\epsilon_\theta(\sqrt{\overline{\alpha}_t}\mathbf{x}_0+\sqrt{1-\overline{\alpha}_t}\epsilon,t)\right\|^2\right],\quad\epsilon\sim\mathcal{N}(0,1) \end{aligned}

  经过这样一番推导之后就是个 L2-loss。网络的输入是一张和噪声线性组合的图片，然后要估计出来这个噪声。

ϵθ(α‾tx0+1−α‾tϵ,t)\epsilon_\theta(\sqrt{\overline{\alpha}_t}\mathbf{x}_0+\sqrt{1-\overline{\alpha}_t}\epsilon,t)

# 五、训练过程

训练过程如上图左边 Algorithm 1 Training 部分：

  1. 从标准高斯分布采样一个噪声ϵ∼N(0,I)\epsilon\sim\mathcal{N}(0,\mathbf{I})；
  2. 通过梯度下降最小化损失∇θ∣ϵ−zθ(αˉtx0+1−αˉtϵ,t)∣2\nabla_\theta|\boldsymbol{\epsilon}-\mathbf{z}\theta(\sqrt{\bar{\alpha}t}x_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)|^2；
  3. 训练到收敛为止；

测试（采样）如上图右边 Algorithm 2 Sampling 部分：

  1. 从标准高斯分布采样一个噪声xT∼N(0,I)x_T\sim\mathcal{N}(0,\mathbf{I})；
  2. 从时间步 TT 开始正向扩散迭代到时间步 11；
  3. 如果时间步不为 11，则从标准高斯分布采样一个噪声z∼N(0,I)z\sim\mathcal{N}(0,\mathbf{I})，否则z=0z=0；
  4. 根据高斯分布计算每个时间步tt 的噪声图；

# 六、代码实现

参考文章：https://www.assemblyai.com/blog/diffusion-models-for-machine-learning-introduction/

import torch
from denoising_diffusion_pytorch import Unet, GaussianDiffusion
model = Unet(
    dim = 64,
    dim_mults = (1, 2, 4, 8)
).cuda()
diffusion = GaussianDiffusion(
    model,
    image_size = 128,
    timesteps = 1000,   # number of steps
    loss_type = 'l1'    # L1 or L2
).cuda()
# 随机样本
training_images = torch.randn(8, 3, 128, 128)
loss = diffusion(training_images)
loss.backward()
sampled_images = diffusion.sample(batch_size = 4)
# 自定义样本
# trainer = Trainer(
#     diffusion,
#     'path/to/your/images',
#     train_batch_size = 32,
#     train_lr = 2e-5,
#     train_num_steps = 700000,         # total training steps
#     gradient_accumulate_every = 2,    # gradient accumulation steps
#     ema_decay = 0.995,                # exponential moving average decay
#     amp = True                        # turn on mixed precision
# )
#
# trainer.train()

      

          
      

  


   


    

  
    
      
    
    更新于
    
  
  
      
        
      
      阅读次数
      
      次