首页 AI

# 一、混淆矩阵

  在机器学习领域，混淆矩阵（Confusion Matrix），又称为可能性矩阵或错误矩阵。混淆矩阵的结构一般如下图表示的方法。

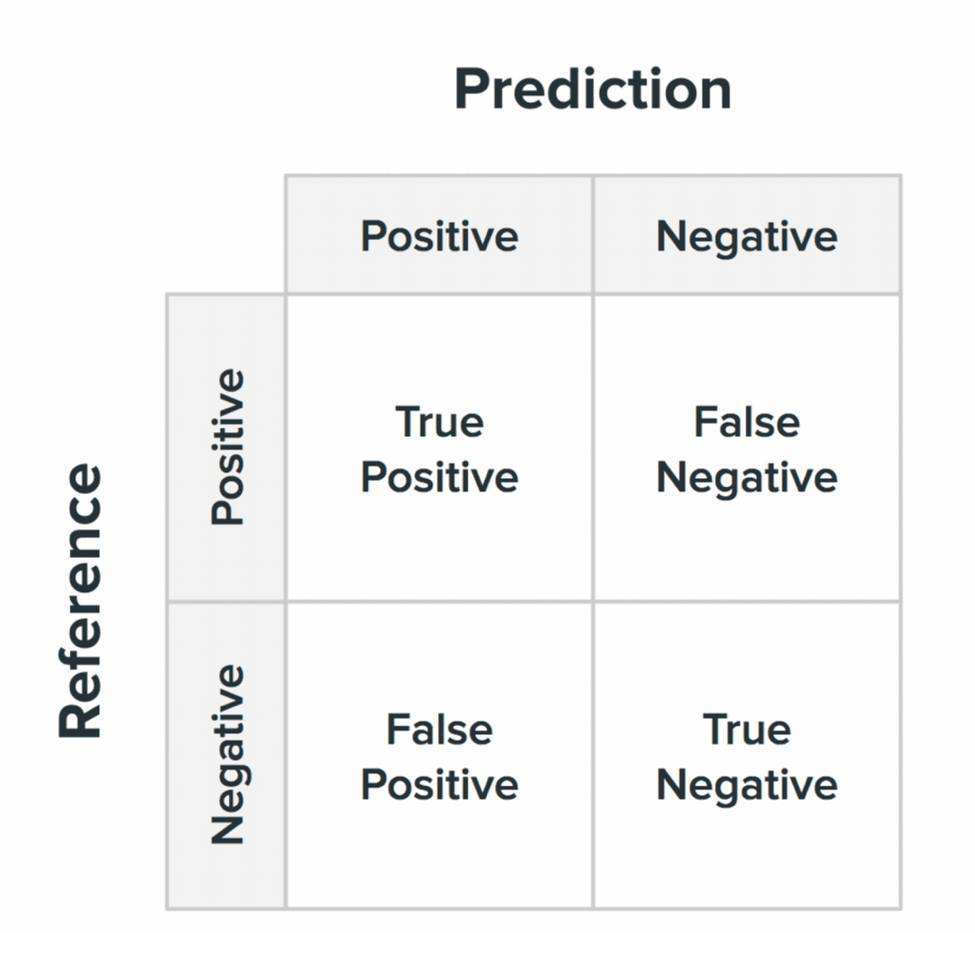
  混淆矩阵要表达的含义：

  • 混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；
  • 每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目；

  每一类的具体定义如下：

  • True Positive（TP）：真正类。样本的真实类别是正类，并且模型识别的结果也是正类。
  • False Negative（FN）：假负类。样本的真实类别是正类，但是模型将其识别为负类。
  • False Positive（FP）：假正类。样本的真实类别是负类，但是模型将其识别为正类。
  • True Negative（TN）：真负类。样本的真实类别是负类，并且模型将其识别为负类。

  该矩阵可用于易于理解的二类分类问题，但通过向混淆矩阵添加更多行和列，可轻松应用于具有 3 个或更多类值的问题。

  记住以下两个关键的理解方法：

  • 根据图片，横着的是数据真实的类别，竖着的是模型预测的类别，先横后竖，先真实类别，后模型预测的类别；
  • True 表示预测正确，False 表示预测错误；Positive 表示模型预测为正样本，Negative 表示模型预测为负样本，所有的单词的意思都是和模型预测有关。

  混淆矩阵是对分类问题的预测结果的总结。使用计数值汇总正确和不正确预测的数量，并按每个类进行细分，这是混淆矩阵的关键所在。混淆矩阵显示了分类模型的在进行预测时会对哪一部分产生混淆。它不仅可以让您了解分类模型所犯的错误，更重要的是可以了解哪些错误类型正在发生。正是这种对结果的分解克服了仅使用分类准确率所带来的局限性。

# 二、从混淆矩阵得到分类指标

  从混淆矩阵当中，可以得到更高级的分类指标：Accuracy（精确率），Precision（正确率或者准确率），Recall（召回率），Specificity（特异性），Sensitivity（灵敏度）。

  对于二分类问题，有如下关系：

样例总数=TP+FP+TN+FN。样例总数 = TP + FP + TN + FN。

# 2.1 准确率（Accuracy）

  准确率是最常用的评价指标，表示模型正确预测的样本占所有样本的比例。计算公式为：

公式：

准确率=分类正确的样本数总样本数准确率=\frac{分类正确的样本数}{总样本数}

Accuracy=TP+TNTP+TN+FP+FNAccuracy = \frac{TP + TN}{TP + TN + FP + FN}

优点：

  • 简单易懂，适用于数据平衡的情况。

缺点：

  • 当数据不平衡时，准确率可能会受到极大影响。例如，在样本类别严重不均的情况下，准确率可能看起来很好，但模型的性能却不理想。

# 2.2 精确率（Precision）

  精确率又称为查准率，表示在所有被模型预测为正类的样本中，真正为正类的比例。精确率可以帮助我们理解模型在预测正类时的准确度。

公式：

精确率=真正类(TP)真正类(TP)+假正类(FP)精确率=\frac{真正类(TP)}{真正类(TP)+假正类(FP)}

Precision=TPTP+FPPrecision = \frac{TP}{TP + FP}

优点：

  • 精确率较高说明模型对正类预测的可信度高。

缺点：

  • 精确率并不关心模型是否漏掉了正类样本。

# 2.3 召回率（Recall）

  召回率又称为查全率，表示在所有实际为正类的样本中，模型预测为正类的比例。召回率衡量模型对正类的识别能力。

公式：

召回率=真正类(TP)真正类(TP)+假负类(FN)召回率=\frac{真正类(TP)}{真正类(TP)+假负类(FN)}

Recall=TPTP+FNRecall = \frac{TP}{TP + FN}

优点：

  • 召回率较高说明模型能够识别大部分的正类样本。

缺点：

  • 召回率较高可能意味着更多的假正例，导致精确率较低。

# 2.4 精确率和召回率的关系

  精确率和召回率是一对矛盾的指标。一般来说，精确率高时，召回率旺旺偏低；召回率高时，精确率往往偏低。作为两大常用的指标，根据不同的任务，具有不同的重要程度。一半来说具有如下规律：

  • 精确率更重要的任务：通常是那些误报代价较高的任务，如垃圾邮件过滤、广告推荐和信息检索。通俗理解：不能多预测，保证模型预测的都是对的（高亮任务需要保证的是精确率，即不能高亮的太多了，要保证高亮的都是对的）
  • 召回率更重要的任务：通常是那些漏掉关键信息会有严重后果的任务，如医疗诊断、欺诈检测和安全监控。通俗理解：可以多预测，只要不漏掉就行。

# 2.5 F1 分数（F1-Score）

  F1 分数是精确率和召回率的调和平均数，结合了精确率和召回率两个指标，能够同时考虑这两者的平衡性。这个指标特别适用于那些对精确率和召回率同等重视的情况，在不均衡数据的场景下尤其有用。

公式：

F1=2×Precision×RecallPrecision+RecallF1 = 2 \times \frac{Precision \times Recall}{Precision + Recall}

  F1 分数的取值范围是 0 到 1，1 表示完美的精确率和召回率，0 则表示两者中至少有一个为零。

优点：

  • F1 分数能够平衡精确率和召回率，适合数据不均衡的情况。

缺点：

  • F1 分数可能无法准确反映精确率和召回率的单独表现，特别是在某些应用场景下，某一指标比另一个更重要。

# 2.5 ROC 曲线 AUC 得分

# （1）ROC 曲线

  许多分类器能够通过输出概率值来量化他们对答案的不确定性。要根据概率计算准确性，您需要一个阈值来决定分类起预测结果是 0 或者 1。AUC 考虑了所有可能的阈值。不同的阈值会导致不同的真正率 (TPR)/ 假正率 (FPR)。随着阈值的降低，分类器会获得更多的真阳性，但也会获得更多的假阳性。它们之间的关系可以绘制出来：

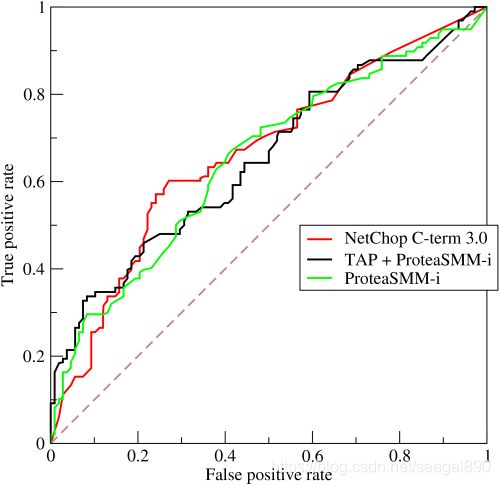
# （2）AUC 得分

  AUC 代表 ROC 曲线下的面积。它是一个介于 0 和 1 之间的数，用于衡量模型整体的分类性能。AUC 的值越接近 1，表示模型的性能越好；AUC 的值越接近 0.5，表示模型的性能没有比随机猜测好多少；如果 AUC 小于 0.5，通常意味着模型做出的预测与实际情况相反。

更新于 阅读次数 次